

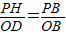 ,得到PH=
,得到PH= (8-x),再根據S△APD=
(8-x),再根據S△APD= S△ABC,就可以求出PC的長.
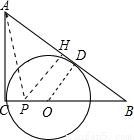
S△ABC,就可以求出PC的長. 解:(1)過點D作DO⊥AB于D,
解:(1)過點D作DO⊥AB于D, ,
,
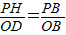 ,
,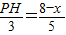 ,
, (8-x),
(8-x), AD•PH=
AD•PH= ×6×
×6× (8-x)=
(8-x)=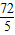 -
- x;
x; S△ABC
S△ABC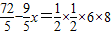
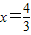 ;
; 時,存在P點,使S△APD=
時,存在P點,使S△APD= S△ABC.
S△ABC.

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com