【答案】
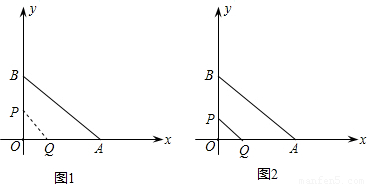
分析:(1)由于A(8,0),B(0,6),∴OB=6,OA=8,AB=10.在前3秒內,點P在OB上,點Q在OA上,設經過t秒,點P,Q位置如圖.則OP=6-2t,OQ=t.∴△OPQ的面積A=

OP•OQ=t(3-t),當t=

時,S
max=

.
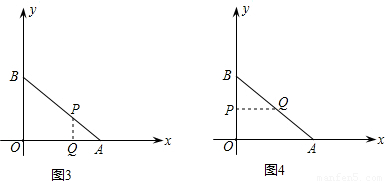
(2)在前10秒內,點P從B開始,經過點O,點A,最后到達AB上,經過的總路程為20;點Q從O開始,經過點A,最后也到達AB上,經過的總路程為10.其中P,Q兩點在某一位置重合,最小距離為0.設在某一位置重合,最小距離為0.
設經過t秒,點Q被點P“追及”(兩點重合),則2t=t+6,∴t=6.∴在前10秒內,P,Q兩點的最小距離為0,點P,Q的相應坐標為(6,0).
(3)①設0≤t<3,則點P在OB上,點Q在OA上,OP=6-2t,OQ=t.若PQ∥AB,則
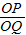
=

,
∴
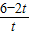
=

,
解得t=
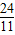
.
此時,P(0,
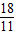
),Q(
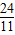
,0).(2分)
②設3≤t≤7,則點P,Q都在OA上,不存在PQ平行于△OAB一邊的情況.
③設7<t<8,則點P在AB上,點Q在OA上,AP=2t-14,AQ=8-t.若PQ∥OB,
則
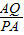
=
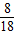
,∴
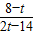
=

,
解得t=
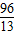
.
此時,P(
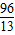
,
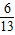
),Q(
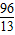
,
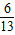
).(2分)
④設8≤t≤12,則兩點P,Q都在AB上,不存在PQ平行于△OAB一邊的情況.
⑤設12<t<15,則點P在OB上、點Q在AB上,BP=2t-24,BQ=18-t.
若PQ∥OA,則
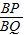
=
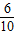
,∴
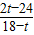
=

,
解得t=
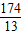
.
此時,P(0,
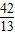
),Q(
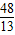
,
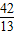
).(2分)
解答:解:(1)∵A(8,0),B(0,6),∴OB=6,OA=8,AB=10.
在前3秒內,點P在OB上,點Q在OA上,設經過t秒,點P,Q位置如圖.
則OP=6-2t,OQ=t.∴△OPQ的面積A=

OP•OQ=t(3-t),(2分)
當t=

時,S
max=

.(2分)
(2)在前10秒內,點P從B開始,經過點O,點A,最后到達AB上,經過的總路程為20;點Q從O開始,經過點A,最后也到達AB上,經過的總路程為10.其中P,Q兩點在某一位置重合,最小距離為0.
設在某一位置重合,最小距離為0.
設經過t秒,點Q被點P“追及”(兩點重合),則2t=t+6,∴t=6.∴在前10秒內,P,Q兩點的最小距離為0,點P,Q的相應坐標為(6,0).(4分)
(3)①設0≤t<3,則點P在OB上,點Q在OA上,OP=6-2t,OQ=t.
若PQ∥AB,則
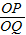
=

,∴
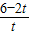
=

,解得t=
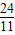
.
此時,P(0,
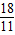
),Q(
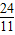
,0).(2分)
②設3≤t≤7,則點P,Q都在OA上,不存在PQ平行于△OAB一邊的情況.
③設7<t<8,則點P在AB上,點Q在OA上,AP=2t-14,AQ=8-t.
若PQ∥OB,則
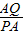
=
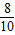
,∴
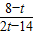
=

,解得t=
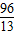
.
此時,P(
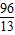
,
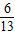
),Q(
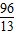
,0).(2分)
④設8≤t≤12,則兩點P,Q都在AB上,不存在PQ平行于△OAB一邊的情況.
⑤設12<t<15,則點P在OB上、點Q在AB上,BP=2t-24,BQ=18-t.
若PQ∥OA,則
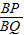
=
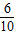
,∴
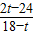
=

,
解得t=
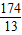
.
此時,P(0,
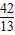
),Q(
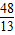
,
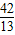
).(2分)
 點評:
點評:此題很復雜,把動點問題與實際相結合,有一定的難度,解答此題的關鍵是分別畫出t在不同階段Q的位置圖,結合相應的圖形解答.


 OP•OQ=t(3-t),當t=
OP•OQ=t(3-t),當t= 時,Smax=
時,Smax= .
.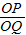 =
= ,
,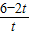 =
= ,
,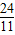 .
.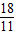 ),Q(
),Q(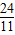 ,0).(2分)
,0).(2分)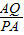 =
=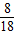 ,∴
,∴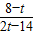 =
= ,
,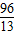 .
.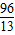 ,
,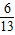 ),Q(
),Q(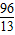 ,
,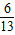 ).(2分)
).(2分)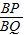 =
=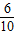 ,∴
,∴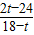 =
= ,
,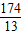 .
.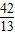 ),Q(
),Q(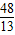 ,
,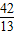 ).(2分)
).(2分) OP•OQ=t(3-t),(2分)
OP•OQ=t(3-t),(2分) 時,Smax=
時,Smax= .(2分)
.(2分)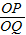 =
= ,∴
,∴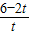 =
= ,解得t=
,解得t=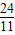 .
.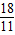 ),Q(
),Q(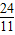 ,0).(2分)
,0).(2分)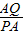 =
=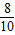 ,∴
,∴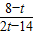 =
= ,解得t=
,解得t=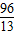 .
.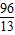 ,
,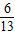 ),Q(
),Q(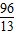 ,0).(2分)
,0).(2分)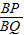 =
=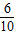 ,∴
,∴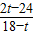 =
= ,
,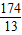 .
.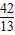 ),Q(
),Q(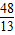 ,
,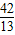 ).(2分)
).(2分)



 ,則AB= .
,則AB= .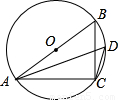
 ,則AB= .
,則AB= .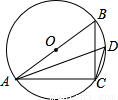

 ,則AB= .
,則AB= .