【題目】函數
和
在第一象限內的圖像如圖，P是 的圖象上一動點， PC⊥ x軸于點 C，交 的圖象于點 A，PD ⊥y 軸于點D，交的圖像于點B，當點P在的圖像上運動時，下列結論錯誤的是（ ）
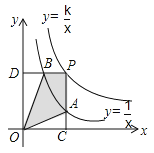
A.△ODB與△OCA的面積相等B.當點 A 是 PC 的中點時，點 B 一定是 PD 的中點
C.
D.當四邊形 OCPD 為正方形時，四邊形 PAOB 的面積最大
科目：初中數學 來源： 題型：
【題目】如圖,AB是⊙0的直徑,點C在⊙0上,D是
中點,若∠BAC=70°,求∠C.
下面是小雯的解法,請幫他補充完整:
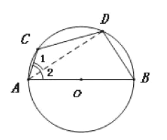
解:在⊙0中,
∵D是的中點
∴BD=CD.
∴∠1=∠2( )(填推理的依據).
∵∠BAC=70°,
∴∠2=35°.
∵AB是⊙0的直徑,
∴∠ADB=90°( )(填推理的依據).
∴∠B=90°-∠2=55°.
∵A、B、C、D四個點都在⊙0上,
∴∠C+∠B=180°( )(填推理的依據).
∴∠C=180°-∠B= (填計算結果).
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商店準備購進
兩種商品，
種商品毎件的進價比
種商品每件的進價多20元，用3000元購進種商品和用1800元購進種商品的數量相同．商店將種商品每件的售價定為80元，種商品每件的售價定為45元．
（1）種商品每件的進價和種商品每件的進價各是多少元？
（2）商店計劃用不超過1560元的資金購進兩種商品共40件，其中種商品的數量不低于種商品數量的一半，該商店有幾種進貨方案？
（3）端午節期間，商店開展優惠促銷活動，決定對每件種商品售價優惠
（
）元，種商品售價不變，在（2）條件下，請設計出銷售這40件商品獲得總利潤最大的進貨方案．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們把對角線互相垂直的四邊形叫做垂直四邊形．
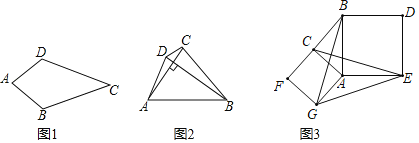
（1）如圖1，在四邊形ABCD中，AB＝AD，CB＝CD，問四邊形ABCD是垂直四邊形嗎？請說明理由；
（2）如圖2，四邊形ABCD是垂直四邊形，求證：AD2+BC2＝AB2+CD2；
（3）如圖3，Rt△ABC中，∠ACB＝90°，分別以AC、AB為邊向外作正方形ACFG和正方形ABDE，連接CE，BG，GE，已知AC＝4，BC＝3，求GE長．
查看答案和解析>>
科目：初中數學 來源： 題型：
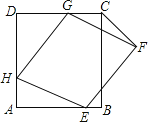
【題目】如圖，菱形EFGH的三個頂點E、G、H分別在正方形ABCD的邊AB、CD、DA上，連接CF．
（1）求證：∠HEA=∠CGF；
（2）當AH=DG時，求證：菱形EFGH為正方形．
查看答案和解析>>
科目：初中數學 來源： 題型：
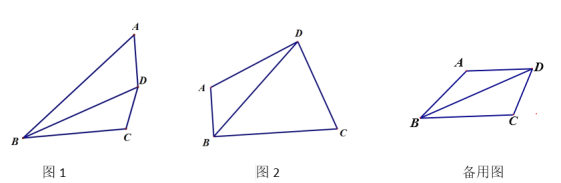
【題目】在四邊形 ABCD 中，BD 平分∠ABC．
（1）如圖 1，若∠BAD=∠BDC，求證：BD2=ABBC；
（2）如圖 2，∠A>90°，∠BAD+∠BDC=180°，
①若∠ABC=90°，AB=
，BC=8，求BD的長；
②若 BC=3CD=3a，BD=9， 則 AB 的長為 ． (用含 a 的代數式表示)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】今年是五四運動100周年，也是中華人民共和國成立70周年，為緬懷五四先驅崇高的愛國情懷和革命精神，巴蜀中學開展了“青春心向黨，建功新時代”為主題的系列紀念活動．歷史教研組也組織了近代史知識競賽，七、八年級各有300名學生參加競賽．為了解這兩個年級參加競賽學生的成績情況，從中各隨機抽取20名學生的成績，并對數據進行了整理和分析（成績得分用
表示，數據分為6組
；
；
；
；
；
）
繪制了如下統計圖表：
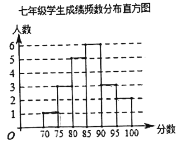
年級 | 平均數 | 中位數 | 眾數 | 極差 |
七年級 | 85.8 |
|
| 26 |
八年級 | 86.2 | 86.5 | 87 | 18 |
七年級測試成績在
、
兩組的是：81 83 83 83 83 86 87 88 88 89 89
根據以上信息，解答下列問題
（1）上表中
_______，
_______．
（2）記成績90分及90分以上為優秀，則估計七年級參加此次知識競賽成績為優秀的學生有多少名？
（3）此次競賽中，七、八兩個年級學生近代史知識掌握更好的是________（填“七”或“八“）年級，并說明理由？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，一次函數y＝2x+b的圖象與x軸的交點為A（2，0），與y軸的交點為B，直線AB與反比例函數y＝
的圖象交于點C（﹣1，m）．
（1）求一次函數和反比例函數的表達式；
（2）直接寫出關于x的不等式2x+b＞的解集；
（3）點P是這個反比例函數圖象上的點，過點P作PM⊥x軸，垂足為點M，連接OP，BM，當S△ABM＝2S△OMP時，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
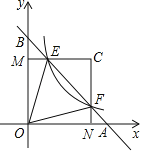
【題目】如圖，在平面直角坐標系中，直線AB與x軸，y軸分別交于A，B，與反比例函數
（k＞0）在第一象限的圖象交于點E，F，過點E作EM⊥y軸于M，過點F作FN⊥x軸于N，直線EM與FN交于點C，若
，則△OEF與△CEF的面積之比是（ ）
A.2：1B.3：1C.2：3D.3：2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
