
【題目】如圖,已知直線l1:y=x+3與x軸交于點A,與y軸交于點B,與直線l2:y=﹣ ![]() x交于點P.直線l3:y=﹣
x交于點P.直線l3:y=﹣ ![]() x+4與x軸交于點C,與y軸交于點D,與直線l1交于點Q,與直線l2交于點R.
x+4與x軸交于點C,與y軸交于點D,與直線l1交于點Q,與直線l2交于點R. 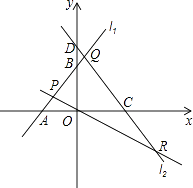
(1)點A的坐標是 , 點B的坐標是 , 點P的坐標是;
(2)將△POB沿y軸折疊后,點P的對應點為P′,試判斷點P′是否在直線l3上,并說明理由;
(3)求△PQR的面積.
【答案】
(1)(﹣3,0);(0,3);(﹣2,1)
(2)解:點P在直線l3上
∵P(﹣2,1),且將△POB沿y軸折疊后,點P與點P關于y軸對稱,
∴P(2,1),
當x=2時,代入y=﹣ ![]() x+4得y=﹣
x+4得y=﹣ ![]() ×2+4=1,
×2+4=1,
∴點P在直線l3上
(3)解:分別過點P作PE⊥x軸于F,過點Q作QF⊥x軸于F,過點R作RG⊥x軸于G,
由  得
得  ,
,
∴Q( ![]() ,
, ![]() ),
),
由  得
得 ![]()
∴R(4,﹣2),
對于y=﹣ ![]() x+4,則y=0得x=
x+4,則y=0得x= ![]() ,
,
∴C( ![]() ,0),
,0),
∴S△AQC= ![]() AC×QF=
AC×QF= ![]() ×(
×( ![]() +3)×
+3)× ![]() =
= ![]() ,S△OCR=
,S△OCR= ![]() OCGR=
OCGR= ![]() ×
× ![]() ×2=
×2= ![]() ,S△AOP=
,S△AOP= ![]() OAPE=
OAPE= ![]() ×3×1=
×3×1= ![]() ,
,
∴S△PQR=S△AQC+S△OCR﹣S△AOP= ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() .
.

【解析】解:(1)∵直線l1:y=x+3與x軸交于點A,與y軸交于點B,
∴令y=0,求得x=﹣3,令x=0,求得y=3,
∴A(﹣3,0)、B(0,3),
∵直線l1與直線l2y=﹣ ![]() x交于點P.
x交于點P.
∴解  得
得 ![]() ,
,
∴P(﹣2,1),
所以答案是:(﹣3,0),(0,3),(﹣2,1);


科目:初中數學 來源: 題型:
【題目】某超市超市準備購進A、B兩種品牌的書包共100個,已知兩種書包的進價如下表所示,設購進A種書包x個,且所購進的兩種書包能全部賣出,獲得的總利潤為y元.
品牌 | 購買個數(個) | 進價(元/個) | 售價(元/個) | 獲利(元) |
A | x | 50 | 60 | __________ |
B | __________ | 40 | 55 | __________ |
(1)將表格的信息填寫完整;
(2)求y關于x的函數表達式;
(3)如果購進兩種書包的總費用不超過4500元且購進B種書包的數量不大于A種書包的3倍,那么超市如何進貨才能獲利最大?并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一粒木質中國象棋棋子“車”,它的正面雕刻一個“車”字,它的反面是平的,將棋子從一定高度下拋,落地反彈后可能是“車”字面朝上,也可能是“車”字面朝下.由于棋子的兩面不均勻,為了估計“車”字面朝上的概率,某實驗小組做了棋子下拋實驗,并把實驗數據整理如下:
實驗次數 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“車”字面朝上的頻數 | 14 | 28 | 38 | 47 | 52 | 66 | 78 | 88 |
相應的頻率 | 0.7 | 0.7 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 | 0.55 |

(1)請將表中數據補充完整,并畫出折線統計圖中的剩余部分.
(2)如果實驗繼續進行下去,根據上表數據,這個實驗的頻率將接近于該事件發生的概率,請估計這個概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線L: ![]() 與x軸、y軸分別交于A、B兩點,在y軸上有一點
與x軸、y軸分別交于A、B兩點,在y軸上有一點
C(0,4),動點M從A點以每秒1個單位的速度沿x軸向左移動。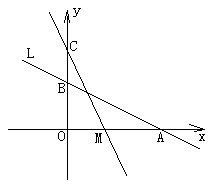
(1)求A、B兩點的坐標;
(2)求△COM的面積S與M的移動時間t之間的函數關系式;
(3)當t為何值時△COM≌△AOB,并求此時M點的坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果線段AB與線段CD沒有交點,則( )
A.線段AB與線段CD一定平行
B.線段AB與線段CD一定不平行
C.線段AB與線段CD可能平行
D.以上說法都不正確
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年,某市發生了嚴重干旱,該市政府號召居民節約用水,為了解居民用水情況,在某小區隨機抽查了10戶家庭的月用水量,結果統計如圖,則關于這10戶家庭的月用水量,下列說法錯誤的是( )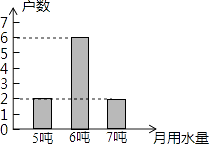
A.眾數是6
B.中位數是6
C.平均數是6
D.方差是4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數y=0.5x+1的圖象與x軸交于點A,與y軸交于點B,二次函數y=0.5x2+bx+c的圖象與一次函數y=0.5x+1的圖象交于點B、C兩點,與x軸交于D、E兩點,且D點坐標為(1,0).
(1)求二次函數的解析式;
(2)在在x軸上有一動點P,從O點出發以每秒1個單位的速度沿x軸向右運動,是否存在動點P,使得△PBC是以P為直角頂點的直角三角形?若存在,求出點P運動時間t的值;若不存在,請說明理由;
(3)若動點P在x軸上,動點Q在射線AC上,同時從A點出發,點P沿x軸正方向以每秒2個單位的速度運動,點Q以每秒a個單位的速度沿射線AC運動,是否存在以A、P、Q為頂點的三角形與△ABD相似?若存在,求a的值;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
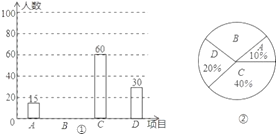
【題目】為推廣陽光體育“大課間”活動,某中學決定在學生中開設A:實心球,B:立定跳遠,C:跳繩,D:跑步四種活動項目.為了了解學生對四種項目的喜歡情況,隨機抽取了部分學生進行調查,并將調查結果繪制成如圖①②的統計圖.請結合圖中的信息解答下列問題:
(1)在這項調查中,共調查了多少名學生?
(2)請計算本項調查中喜歡“立定跳遠”的學生人數和所占百分比,并將兩幅統計圖中的B補充完整;
(3)若調查到喜歡“跳繩”的5名學生中有3名男生,2名女生.現從這5名學生中任意抽取2名學生.請用畫樹狀圖或列表的方法,求出剛好抽到同性別學生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com