Question

（1）如圖，在△ABC中，∠BAC=90°，AB=A C，點D在BC上，且BD=BA，點E在BC的延長線上，且CE=CA． 試求∠DAE的度數．

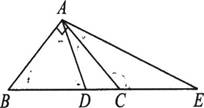
(2)如果把第(1)題中“AB=AC”的條件去掉，其余條件不變，那么∠DAE的度數會改變嗎?

(3)如果把第(1)題中“∠BA C=90°”的條件改為“∠BAC>90°”。其余條件不變，那么∠DAE與∠BAC有怎樣的大小關系? 并說明理由。

 

Answer 1

（1）45度（2）不改變(3)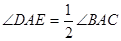

解析:解：（1）∵AB＝AC，∠BAC＝90°

           ∴∠B＝∠ACB＝45°     …………………………………………1′

           ∵AB＝BD，AC＝CE，

           ∴∠BAD＝∠BDA，∠E＝∠CAE

           ∴……4′

          在△ABE中，∠BAE=180°-∠B-∠E=112.5°，

∴∠DAE=∠BAE-∠BAD=112.5°-67.5°=45度……………6′

（2）不改變．

設∠CAE=x，

∵CA=CE，

∴∠E=∠CAE=x，

∴∠ACB=∠CAE+∠E=2x，

在△ABC中，∠BAC=90°，

∴∠B=90°-∠ACB=90°-2x，

∵BD=BA，

∴∠BAD=∠BDA=（180°-∠B）=x+45°，

在△ABE中，∠BAE=180°-∠B-∠E，

=180°-（90°-2x）-x=90°+x，

∴∠DAE=∠BAE-∠BAD，

=（90°+x）-（x+45°）=45° ………………………………………7′

 （3）       ………………………………………8′

  設∠BAC＝α，因為

     所以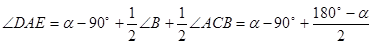

             ＝      ………………………………………10′

（1）要求∠DAE，必先求∠BAD和∠CAE，由∠BAC=90°，AB=AC，可求∠B=∠ACB=45°，又因為BD=BA，可求∠BAD=∠BDA=67.5°，再由CE=CA，可求∠CAE=∠E=22.5°，所以∠DAE=∠BAE-∠BAD=112.5°-67.5°=45度；

（2）先設∠CAE=x，由已知CA=CE可求∠ACB=∠CAE+∠E=2x，∠B=90°-2x，又因為BD=BA，所以∠BAD=∠BDA=x+45°，再根據三角形的內角和是180°，可求∠BAE=90°+x，即∠DAE=∠BAE-∠BAD=（90°+x）-（x+45°）=45度；

（3）可設∠BAC＝α，則 ＝