【題目】重慶育才中學需要為老校友們訂制
周年紀念吉祥物“陶娃”，原計劃訂
份，每份
元，訂制公司表示：如果多訂，可以優惠.根據校慶當天前來的校友數量，學校最終訂了
份，并按原價八折購買，但訂制公司獲得了同樣的利潤.
（1）求訂制公司生產每套“陶娃”的成本；
（2）求訂制公司獲得的利潤.
世紀百通主體課堂小學課時同步達標系列答案
世紀百通優練測系列答案
百分學生作業本題練王系列答案科目：初中數學 來源： 題型：
【題目】“萬州古紅桔”原名“萬縣紅桔”，古稱丹桔（以下簡稱為紅桔），種植距今至少已有一千多年的歷史，“玫瑰香橙”（源自意大利西西里島塔羅科血橙，以下簡稱香橙）現已是萬州柑橘發展的主推品種之一．某水果店老板在2017年11月份用15200元購進了400千克紅桔和600千克香橙，已知香橙的每千克進價比紅桔的每千克進價2倍還多4元．
（1）求11月份這兩種水果的進價分別為每千克多少元？
（2）時下正值柑橘銷售旺季，水果店老板決定在12月份繼續購進這兩種水果，但進入12月份，由于柑橘的大量上市，紅桔和香橙的進價都有大幅下滑，紅桔每千克的進價在11月份的基礎上下降了
m%，香橙每千克的進價在11月份的基礎上下降了m%，由于紅桔和“玫瑰香橙”都深受庫區人民歡迎，實際水果店老板在12月份購進的紅桔數量比11月份增加了
m%，香橙購進的數量比11月份增加了2m%，結果12月份所購進的這兩種柑橘的總價與11月份所購進的這兩種柑橘的總價相同，求m的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料：我們知道：如果點A.B在數軸上分別表示有理數a、b，那么A.B兩點之間的距離表示為AB，在數軸上A.B兩點之間的距離AB=|ab|.
根據上述材料，利用數軸解答下列問題：
(1)如果點A在數軸上表示2，將點A先向左平移2個單位長度，再向右移動7個單位長度，那么終點B在數軸上表示的數是___；
(2)數軸上表示x和1的兩個點之間的距離是___；
(3)若|x3|+|x+2|=7，則x的值是___；
(4)在(1)的條件下，設點P在數軸上表示的數為x，當|PA||PB|=2時，則x的值是___.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某專賣店正在開展“感恩十年，童行有你”促銷活動一次性購物不超過
元不享受優惠；一次性購物超過元但不超過
元，超過元的部分九折優惠；一次性購物超過元一律八折.在活動期間，張三兩次購物分別付款
元、
元，若張三選擇這兩次購物合并成一次性付款可以節省___________元.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,正方形
的邊長為2, 
邊在
軸上, 的中點與原點
重合,過定點
與動點
的直線
記作
.
（1）若的解析式為
，判斷此時點
是否在直線上，并說明理由；
（2）當直線與
邊有公共點時，求
的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
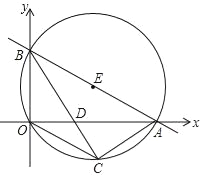
【題目】直線y=﹣
x+
分別與x軸、y軸交于A、B兩點，⊙E經過原點O及A、B兩點，C是⊙E上一點，連接BC交OA于點D，∠COD=∠CBO．
（1）求A、B、C三點坐標；
（2）求經過O、C、A三點的拋物線解析式；
（3）直線AB上是否存在點P，使得△COP的周長最小？若存在，請求出P點坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】重慶市第八中學校為給學生營造良好舒適的休息環境，決定改造校園內的—小花園，如圖是該花園的平面示意圖，它是由
個正方形拼成的長方形用以種植六種不同的植物，已知中間最小的正方形
的邊長是
米，正方形
、
邊長相等.請根據圖形特點求出該花園的總面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
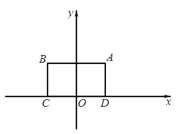
【題目】對于⊙P及一個矩形給出如下定義：如果⊙P上存在到此矩形四個頂點距離都相等的點，那么稱⊙P是該矩形的“等距圓”．如圖，在平面直角坐標系xOy中，矩形ABCD的頂點A的坐標為（
，
），頂點C、D在x軸上，且OC=OD.
（1）當⊙P的半徑為4時，
①在P1（
，
），P2（
，
），P3（
，
）中可以成為矩形ABCD的“等距圓”的圓心的是 ；
②如果點P在直線
上，且⊙P是矩形ABCD的“等距圓”，求點P的坐標；
（2）已知點P在
軸上，且⊙P是矩形ABCD的“等距圓”，如果⊙P與直線AD沒有公共點，直接寫出點P的縱坐標m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
