
已知:反比例函數![]() 和
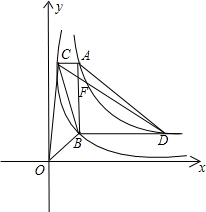
和![]() 在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在
在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在![]() 的圖象上,AB∥y軸,與
的圖象上,AB∥y軸,與![]() 的圖象交于點B,AC、BD與x軸平行,分別與
的圖象交于點B,AC、BD與x軸平行,分別與![]() 、
、![]() 的圖象交于點C、D.
的圖象交于點C、D.
(1)若點A的橫坐標為2,求直線CD的解析式:
(2)若點A的橫坐標為m,梯形ACBD的對角線的交點F,求![]() 的值.
的值.

考點:
反比例函數綜合題.
專題:
綜合題.
分析:
(1)先利用點A在y=![]() 的圖象上可確定A點坐標為(2,4),則根據AC∥x軸,AB∥y軸得到C點的縱坐標為4,B點的橫坐標為2,再利用C、B在y=
的圖象上可確定A點坐標為(2,4),則根據AC∥x軸,AB∥y軸得到C點的縱坐標為4,B點的橫坐標為2,再利用C、B在y=![]() 的圖象上可確定C點坐標為(
的圖象上可確定C點坐標為(![]() ,4),B點坐標為(2,1);由于BD∥x軸,則D點的縱坐標與B的縱坐標相等,根據D點在y=
,4),B點坐標為(2,1);由于BD∥x軸,則D點的縱坐標與B的縱坐標相等,根據D點在y=![]() 的圖象上可確定D點坐標為(8,1),然后利用待定系數法求出直線CD的解析式;
的圖象上可確定D點坐標為(8,1),然后利用待定系數法求出直線CD的解析式;
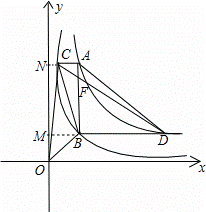
(2)作CM⊥y軸于M,BN⊥y軸于N,與(1)的方法一樣可確定A點坐標為(m,![]() ),C點坐標為(
),C點坐標為(![]() ,
,![]() ),B點坐標為(m,
),B點坐標為(m,![]() ),D點坐標為(4m,
),D點坐標為(4m,![]() ),根據比例系數的幾何意義得到S△OCN=S△OBM=1,根據梯形的面積公式得到S梯形BMNC=
),根據比例系數的幾何意義得到S△OCN=S△OBM=1,根據梯形的面積公式得到S梯形BMNC=![]() ,S梯形ACBD=
,S梯形ACBD=![]() ;再利用S四邊形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM得S△OBC=S梯形BMNC=
;再利用S四邊形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM得S△OBC=S梯形BMNC=![]() ,最后計算
,最后計算![]() 的值.
的值.
解答:
解:(1)把x=2代入y=![]() 得y=4,則A點坐標為(2,4),
得y=4,則A點坐標為(2,4),
∵AC∥x軸,AB∥y軸,
∵C點的縱坐標為4,B點的橫坐標為2,
把y=4代入y=![]() 得x=
得x=![]() ;把x=2代入y=
;把x=2代入y=![]() 得y=1,
得y=1,
∴C點坐標為(![]() ,4),B點坐標為(2,1),
,4),B點坐標為(2,1),
∵BD∥x軸,
∴D點的縱坐標與B的縱坐標相等,
把y=1代入y=![]() 得x=8,
得x=8,
∴D點坐標為(8,1),
設直線DC的解析式為y=kx+b,
把C(![]() ,4)、D(8,1)代入
,4)、D(8,1)代入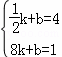 ,解得
,解得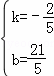 ,
,
∴直線DC的解析式為y=﹣![]() x+
x+![]() ;(2)作CM⊥y軸于M,BN⊥y軸于N,如圖,
;(2)作CM⊥y軸于M,BN⊥y軸于N,如圖,
當點A的橫坐標為m,與(1)的方法一樣可確定A點坐標為(m,![]() ),C點坐標為(
),C點坐標為(![]() ,
,![]() ),B點坐標為(m,
),B點坐標為(m,![]() ),D點坐標為(4m,
),D點坐標為(4m,![]() ),
),
∴AC=m﹣![]() =
=![]() ,BD=4m﹣m=3m,AB=
,BD=4m﹣m=3m,AB=![]() ﹣
﹣![]() =
=![]() ,
,
∴S梯形ACBD=![]() (
(![]() +3m)•
+3m)•![]() =
=![]() ;
;
∵S△OCN=S△OBM=![]() ×2=1,S梯形BMNC=
×2=1,S梯形BMNC=![]() (
(![]() +m)•
+m)•![]() =
=![]() ,
,
而S四邊形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM,
∴S△OBC=S梯形BMNC=![]() ,
,
∴![]() =
=![]() =
=![]() .
.
點評:
本題考查了反比例函數的綜合題:掌握反比例函數圖象上點的坐標特征、比例系數的幾何意義和待定系數法求函數的解析式;記住梯形的面積公式和運用幾何圖形的面積和差求不規則幾何圖形的面積.


科目:初中數學 來源: 題型:解答題
 已知:反比例函數
已知:反比例函數 和
和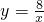 在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在
在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在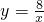 的圖象上,AB∥y軸,與
的圖象上,AB∥y軸,與 的圖象交于點B,AC、BD與x軸平行,分別與
的圖象交于點B,AC、BD與x軸平行,分別與 、
、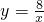 的圖象交于點C、D.
的圖象交于點C、D.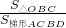 的值.
的值.查看答案和解析>>
科目:初中數學 來源:第20章《二次函數和反比例函數》常考題集(44):20.7 反比例函數的圖象、性質和應用(解析版) 題型:解答題
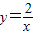 和
和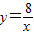 在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在
在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在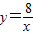 的圖象上,AB∥y軸,與
的圖象上,AB∥y軸,與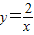 的圖象交于點B,AC、BD與x軸平行,分別與
的圖象交于點B,AC、BD與x軸平行,分別與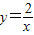 ,
,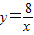 的圖象交于點C、D.
的圖象交于點C、D.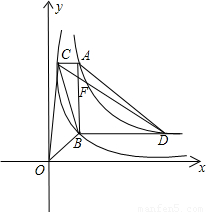
查看答案和解析>>
科目:初中數學 來源:2012年北京市中考數學二模練習試卷(二)(解析版) 題型:解答題
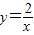 和
和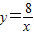 在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在
在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在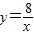 的圖象上,AB∥y軸,與
的圖象上,AB∥y軸,與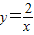 的圖象交于點B,AC、BD與x軸平行,分別與
的圖象交于點B,AC、BD與x軸平行,分別與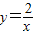 ,
,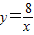 的圖象交于點C、D.
的圖象交于點C、D.
查看答案和解析>>
科目:初中數學 來源:2012年浙江省杭州市文瀾中學中考數學模擬試卷(解析版) 題型:解答題
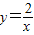 和
和 在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在
在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在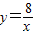 的圖象上,AB∥y軸,與
的圖象上,AB∥y軸,與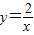 的圖象交于點B,AC、BD與x軸平行,分別與
的圖象交于點B,AC、BD與x軸平行,分別與 ,
,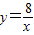 的圖象交于點C、D.
的圖象交于點C、D.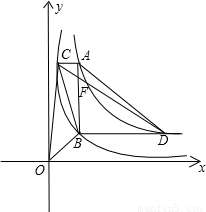
查看答案和解析>>
科目:初中數學 來源:2010年吉林省琿春市琿春四中中考數學模擬試卷(解析版) 題型:解答題
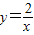 和
和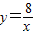 在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在
在平面直角坐標系xOy第一象限中的圖象如圖所示,點A在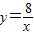 的圖象上,AB∥y軸,與
的圖象上,AB∥y軸,與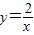 的圖象交于點B,AC、BD與x軸平行,分別與
的圖象交于點B,AC、BD與x軸平行,分別與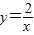 ,
, 的圖象交于點C、D.
的圖象交于點C、D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com