
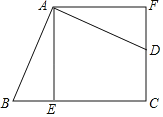
【題目】如圖,四邊形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△ABE繞著點A旋轉后能與△ADF重合,若AF=5cm,則四邊形ABCD的面積為_____.
【答案】25cm2
【解析】
根據垂直的定義可得∠AEB=∠AEC=90°,根據旋轉變換只改變圖形的位置不改變圖形的形狀與大小可得△ADF和△ABE全等,根據全等三角形對應角相等可得∠AEB=∠F,全等三角形對應邊相等可得AE=AF,然后證明四邊形是矩形,再根據鄰邊相等的矩形是正方形可得四邊形AECF是正方形,然后根據正方形的面積公式列式計算即可得解.
解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∵AB=AD,△BEA旋轉后能與△DFA重合,
∴△ADF≌△ABE,
∴∠AEB=∠F,AE=AF,
∵∠C=90°,
∴∠AEC=∠C=∠F=90°,
∴四邊形AECF是矩形,
又∵AE=AF,
∴矩形AECF是正方形,
∵AF=5cm,
∴四邊形ABCD的面積=四邊形AECF的面積=52=25cm2.
故答案為:25cm2.


 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案科目:初中數學 來源: 題型:
【題目】閱讀與思考:
因式分解----“分組分解法”:分組分解法指通過分組分解的方式來分解用提公因式法和公式法無法直接分解的多項式,比如,四項的多項式一般按照“兩兩”分組或“三一”分組進行分組分解.分析多項式的特點,恰當的分組是分組分解法的關鍵.
例1:“兩兩”分組:
![]()
![]()
![]()
![]()
我們把![]() 和
和![]() 兩項分為一組,
兩項分為一組,![]() 和
和![]() 兩項分為一組,分別提公因式,立即解除了困難.同樣.這道題也可以這樣做:
兩項分為一組,分別提公因式,立即解除了困難.同樣.這道題也可以這樣做:
![]()
![]()
![]()
![]()
例2:“三一”分組:
![]()
![]()
![]()
我們把![]() ,
,![]() ,
,![]() 三項分為一組,運用完全平方公式得到
三項分為一組,運用完全平方公式得到![]() ,再與-1用平方差公式分解,問題迎刃而解.
,再與-1用平方差公式分解,問題迎刃而解.
歸納總結:用分組分解法分解因式的方法是先恰當分組,然后用提公因式法或運用公式法繼續分解.
請同學們在閱讀材料的啟發下,解答下列問題:
(1)分解因式:
①![]() ;
;
②![]()
(2)若多項式![]() 利用分組分解法可分解為
利用分組分解法可分解為![]() ,請寫出
,請寫出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
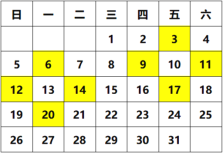
【題目】在日歷上,我們可以發現其中某些數滿足一定的規律,如圖是2020年1月份的日歷.如圖所選擇的兩組四個數,分別將每組數中相對的兩數相乘,再相減,例如:9×11﹣3×17= ,12×14﹣6×20= ,不難發現,結果都是 .
(1)請將上面三個空補充完整;
(2)請你利用整式的運算對以上規律進行證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
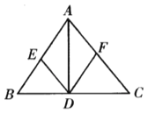
【題目】如圖,已知:AD是△ABC的角平分線,DE//AC交AB于E,DF//AB交AC于F,
(1)求證:四邊形AEDF是菱形;
(2)當△ABC滿足什么條件時,四邊形AEDF是正方形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
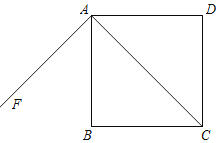
【題目】如圖,正方形ABCD中,對角線AC=8cm.射線AF⊥AC,垂足為A.動點P從點C出發在CA上運動,動點Q從點A出發在射線AF上運動,兩點的運動速度都是2cm/s.若兩點同時出發,多少時間后,四邊形AQBP是特殊四邊形?請說明特殊四邊形的名稱及理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景:如圖1,在正方形ABCD的內部,作∠DAE=∠ABF=∠BCG=∠CDH,根據三角形全等的條件,易得△DAE≌△ABF≌△BCG≌△CDH,從而得四邊形EFGH是正方形.
類比探究:如圖2,在正△ABC的內部,作∠1=∠2=∠3,AD,BE,CF兩兩相交于D,E,F三點(D,E,F三點不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,請選擇其中一對進行證明;
(2)△DEF是否為正三角形?請說明理由;
(3)如圖3,進一步探究發現,△ABD的三邊存在一定的等量關系,設BD=a,AD=b,AB=c,請探索a,b,c滿足的等量關系.
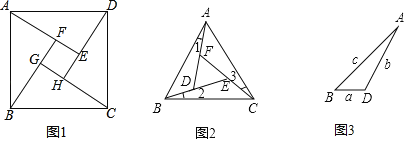
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我校圖書館大樓工程在招標時,接到甲乙兩個工程隊的投標書,每施工一個月,需付甲工程隊工程款16萬元,付乙工程隊12萬元。工程領導小組根據甲乙兩隊的投標書測算,可有三種施工方案:
(1)甲隊單獨完成此項工程剛好如期完工;
(2)乙隊單獨完成此項工程要比規定工期多用3個月;
(3)若甲乙兩隊合作2個月,剩下的工程由乙隊獨做也正好如期完工。
你覺得哪一種施工方案最節省工程款,說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是拋物線y=ax2+bx+c(a≠0)的部分圖象,其頂點坐標為(1,n),拋物線與x軸的一個交點在點(3,0)和(4,0)之間.則下列結論

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有兩個不相等的實數根.
其中正確結論的個數是( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com