
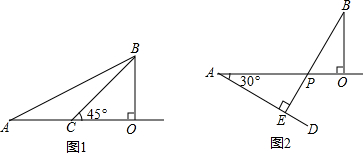
 ≈1.414,
≈1.414, ≈1.732,
≈1.732, ≈2.236,
≈2.236, ≈2.449)
≈2.449)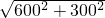 =300
=300 (cm).
(cm). ÷10≈300×2.236÷10≈67(秒).
÷10≈300×2.236÷10≈67(秒).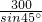 =300
=300 (cm)
(cm) ÷10≈15+42.42≈57(秒).
÷10≈15+42.42≈57(秒). =
=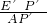 ,∴EP=
,∴EP=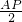 ,E′P′=
,E′P′=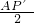 .
. BE(秒),
BE(秒), (E′P′+P′B)(秒).
(E′P′+P′B)(秒). BE<
BE< (E′P′+P′B).
(E′P′+P′B).

 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:初中數學 來源: 題型:

| 2 |
| 3 |
| 5 |
| 6 |
查看答案和解析>>
科目:初中數學 來源:四川省中考真題 題型:解答題
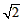 ≈1.414,
≈1.414,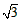 ≈1.732,
≈1.732,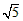 ≈2.236,
≈2.236,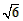 ≈2.449)
≈2.449) 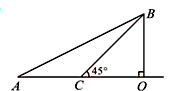
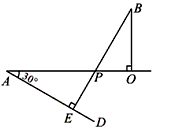
查看答案和解析>>
科目:初中數學 來源:2012年四川省資陽市中考數學模擬試卷(三)(解析版) 題型:解答題
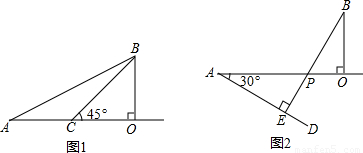
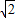 ≈1.414,
≈1.414,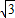 ≈1.732,
≈1.732,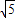 ≈2.236,
≈2.236, ≈2.449)
≈2.449)查看答案和解析>>
科目:初中數學 來源:2011-2012學年四川省資陽市安岳縣魚龍九義校九年級(下)第一次月考數學試卷(解析版) 題型:解答題
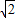 ≈1.414,
≈1.414,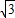 ≈1.732,
≈1.732,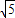 ≈2.236,
≈2.236,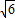 ≈2.449)
≈2.449)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com