科目：初中數學 來源： 題型：
如果二次函數的二次項系數為l，則此二次函數可表示為y=x2+px+q，我們稱[p，q]為此函數的特征數，如函數y=x2+2x+3的特征數是[2，3]．
（1）若一個函數的特征數為[﹣2，1]，求此函數圖象的頂點坐標．
（2）探究下列問題：
①若一個函數的特征數為[4，﹣1]，將此函數的圖象先向右平移1個單位，再向上平移1個單位，求得到的圖象對應的函數的特征數．
②若一個函數的特征數為[2，3]，問此函數的圖象經過怎樣的平移，才能使得到的圖象對應的函數的特征數為[3，4]？
查看答案和解析>>
科目：初中數學 來源： 題型：
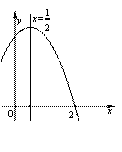
如圖，二次函數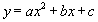
(a≠0)圖象的一部分，對稱軸為x=
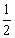，且經過點（2，0）.下列說法：①abc <0，②a+b=0，③4a+2b+c<0，④若（-2，y1）（
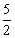，y2）是拋物線上的兩點，則y1＜y2，其中說法正確的是 ( )
A．①②④ B．③④ C．①③④ D．①②
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
在等腰直角三角形ABC中，∠BAC=90°，AB=AC，直線MN過點A且MN∥BC.以點B為一銳角頂點作Rt△BDE，∠BDE=90°，且點D在直線MN上（不與點A重合）.如圖1，DE與AC交于點P，易證：BD=DP.(無需寫證明過程)
（1）在圖2中，DE與CA延長線交于點P，BD=DP是否成立？如果成立，請給予
證明，如果不成立，請說明理由；
（2）在圖3中，DE與AC延長線交于點P，BD與DP是否相等？請直接寫出你的結論，無需證明.
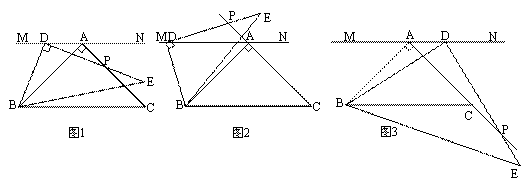
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，已知c＜0，拋物線y=x2+bx+c與x軸交于A（x1，0），B（x2，0）兩點（x2＞x1），與y軸交于點C．
（1）若x2=1，BC=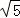
，求函數y=x2+bx+c的最小值；
（2）過點A作AP⊥BC，垂足為P（點P在線段BC上），AP交y軸于點M．若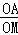
=2，求拋物線y=x2+bx+c頂點的縱坐標隨橫坐標變化的函數解析式，并直接寫出自變量的取值范圍．
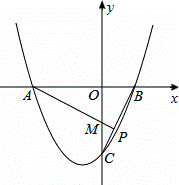
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，則
的值為______．
