
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,在以
,在以![]() 的中點
的中點![]() 為坐標原點,
為坐標原點,![]() 所在直線為
所在直線為![]() 軸建立的平面直角坐標系中,將
軸建立的平面直角坐標系中,將![]() 繞點
繞點![]() 順時針旋轉,使點
順時針旋轉,使點![]() 旋轉至
旋轉至![]() 軸的正半軸上的點
軸的正半軸上的點![]() 處,若
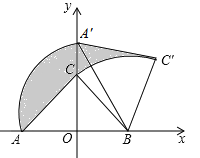
處,若![]() ,則圖中陰影部分面積為________.
,則圖中陰影部分面積為________.
【答案】![]()
【解析】
根據等腰直角三角形的性質求出AB,再根據旋轉的性質可得A′B=AB,然后求出∠OA′B=30°,再根據直角三角形兩銳角互余求出∠A′BA=60°,即旋轉角為60°,再根據S陰影=S扇形ABA′+S△A′BC′-S△ABC-S扇形CBC′=S扇形ABA′-S扇形CBC′,然后利用扇形的面積公式列式計算即可得解.
解:∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴AB=2OA=2OB=4,BC=2![]() ,
,
∵△ABC繞點B順時針旋轉點A在A′處,
∴BA′=AB,
∴BA′=2OB,
∴∠OA′B=30°,
∴∠A′BA=60°,
即旋轉角為60°,
S陰影=S扇形ABA′+S△A′BC′-S△ABC-S扇形CBC′,
=S扇形ABA′-S扇形CBC′,
= ![]() .
.
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】定義:
我們知道,四邊形的一條對角線把這個四邊形分成了兩個三角形,如果這兩個三角形相似(不全等),我們就把這條對角線叫做這個四邊形的“相似對角線”.
理解:
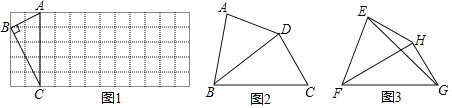
(1)如圖1,已知Rt△ABC在正方形網格中,請你只用無刻度的直尺在網格中找到一點D,使四邊形ABCD是以AC為“相似對角線”的四邊形(保留畫圖痕跡,找出3個即可);
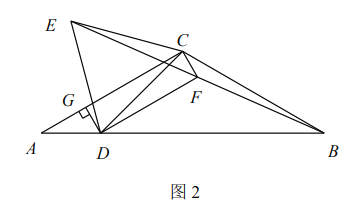
(2)如圖2,在四邊形ABCD中,∠ABC=80°,∠ADC=140°,對角線BD平分∠ABC.
求證:BD是四邊形ABCD的“相似對角線”;
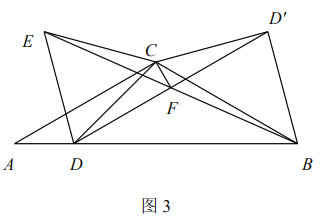
(3)如圖3,已知FH是四邊形EFCH的“相似對角線”,∠EFH=∠HFG=30°,連接EG,若△EFG的面積為2![]() ,求FH的長.
,求FH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC是等邊三角形,點P在射線AC上(點P與點A、點C不重合),點D在線段BC的延長線上,且AP=CD,△PCD′與△PCD關于直線AC對稱.
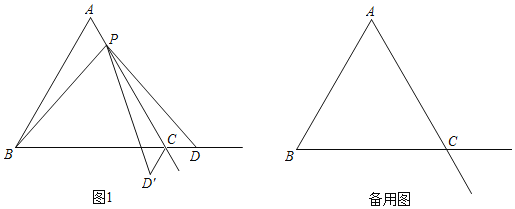
(1)如圖1,當點P在線段AC上時,
①求證:PB=PD;
②請求出∠BPD′的度數;
(2)當點P在射線AC上運動時,請直接回答:
①PB=PD是否仍然成立?
②∠BPD′的度數是否發(fā)生變化?
(3)將△PCD′繞點P順時針旋轉,在旋轉的過程中,PD′與PB能否重合?若能重合,請直接寫出旋轉的角度;若不能重合,請說明理由;
(4)若AB=4,當點P為AC邊的中點時,請直接寫出PD'的長
查看答案和解析>>
科目:初中數學 來源: 題型:
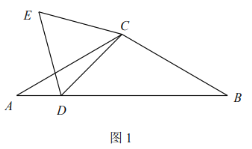
【題目】如圖,路燈下,廣告標桿AB的影子是BC,小明(用線段DE表示)的影子是EF,在M處有一棵樹,它的影子是MN.
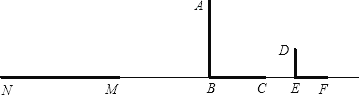
(1)請在圖中畫出表示樹高的線段.(不寫作法,保留作圖痕跡)
(2)若已知點N、F到路燈的底部距離相等,小明身高1.6米,影長EF為1.8米,樹的影長MN是6米,請計算樹的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角梯形ABCD中,∠ADC=90°,AD∥BC,點E在BC上,點F在AC上,∠DFC=∠AEB.
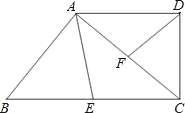
(1)求證:△ADF∽△CAE;
(2)當AD=8,DC=6,點E、F分別是BC、AC的中點時,求BC的長?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 和
和![]() 中,
中,![]() ,點
,點![]() 為射線
為射線![]() ,
,![]() 的交點.
的交點.
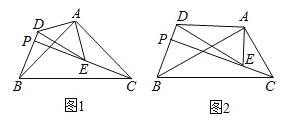
(1)問題提出:如圖1,若![]() ,
,![]() .
.
①![]() 與
與![]() 的數量關系為________;
的數量關系為________;
②![]() 的度數為________.
的度數為________.
(2)猜想論證:如圖2,若![]() ,則(1)中的結論是否成立?請說明理由.
,則(1)中的結論是否成立?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題的提出:
如果點P是銳角△ABC內一動點,如何確定一個位置,使點P到△ABC的三頂點的距離之和PA+PB+PC的值為最小?
問題的轉化:
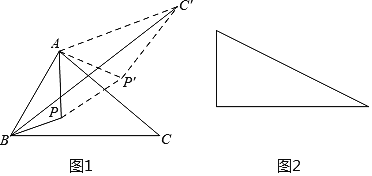
(1)把ΔAPC繞點A逆時針旋轉60度得到![]() 連接
連接![]() 這樣就把確定PA+PB+PC的最小值的問題轉化成確定
這樣就把確定PA+PB+PC的最小值的問題轉化成確定![]() 的最小值的問題了,請你利用如圖證明:
的最小值的問題了,請你利用如圖證明:
![]() ;
;
問題的解決:
(2)當點P到銳角△ABC的三項點的距離之和PA+PB+PC的值為最小時,請你用一定的數量關系刻畫此時的點P的位置:_____________________________;
問題的延伸:
(3)如圖是有一個銳角為30°的直角三角形,如果斜邊為2,點P是這個三角形內一動點,請你利用以上方法,求點P到這個三角形各頂點的距離之和的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() , 點
, 點![]() 是
是![]() 邊上一點,連接
邊上一點,連接![]() ,以
,以![]() 為邊作等邊
為邊作等邊![]() .
.
![]() 如圖1,若
如圖1,若![]() 求等邊
求等邊![]() 的邊長;
的邊長;
![]() 如圖2,點
如圖2,點![]() 在
在![]() 邊上移動過程中,連接
邊上移動過程中,連接![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() .
.
①求證:![]() ;
;
②如圖3,將![]() 沿
沿![]() 翻折得
翻折得![]() ,連接
,連接![]() ,直接寫出
,直接寫出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點E,F分別是邊AD,BC的中點,連接DF,過點E作EH⊥DF,垂足為H,EH的延長線交DC于點G.
(1)猜想DG與CF的數量關系,并證明你的結論;
(2)過點H作MN∥CD,分別交AD,BC于點M,N,若正方形ABCD的邊長為10,點P是MN上一點,求△PDC周長的最小值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com