
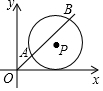
 如圖,在平面直角坐標系中,點P的坐標為(a,5),半徑為5的⊙P交直線y=x于點A,B,若弦AB=8,-則a的值為5+3$\sqrt{2}$.
如圖,在平面直角坐標系中,點P的坐標為(a,5),半徑為5的⊙P交直線y=x于點A,B,若弦AB=8,-則a的值為5+3$\sqrt{2}$. 分析 作PC⊥y軸于C,交AB于D,作PE⊥AB于E,連結PB,由于OC=5,PC=a,易得D點坐標為(5,5),則△OCD為等腰直角三角形,△PED也為等腰直角三角形.由PE⊥AB,根據垂徑定理得AE=BE=$\frac{1}{2}$AB=4,在Rt△PBE中,利用勾股定理可計算出PE=3,則PD=$\sqrt{2}$PE=3$\sqrt{2}$,所以a=5+3$\sqrt{2}$.
解答 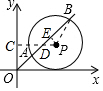 解:作PC⊥y軸于C,交AB于D,作PE⊥AB于E,連結PB,如圖,
解:作PC⊥y軸于C,交AB于D,作PE⊥AB于E,連結PB,如圖,
∵⊙P的圓心坐標是(a,5),
∴OC=5,PC=a,
把x=5代入y=x得y=5,
∴D點坐標為(5,5),
∴CD=5,
∴△OCD為等腰直角三角形,
∴△PED也為等腰直角三角形,
∵PE⊥AB,
∴AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
在Rt△PBE中,PB=5,
∴PE=$\sqrt{B{P}^{2}-B{E}^{2}}$=3,
∴PD=$\sqrt{2}$PE=3$\sqrt{2}$,
∴a=5+3$\sqrt{2}$.
故答案為:5+3$\sqrt{2}$.
點評 本題考查了圓的綜合題,垂徑定理:垂直于弦的直徑平分這條弦,并且平分弦所對的兩條弧.也考查了勾股定理和等腰直角三角形的性質.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 超速行駛是引發交通事故的主要原因.上周末,小明和三位同學嘗試用自己所學的知識檢測車速,如圖,觀測點設在到縣城城南大道的距離為100米的點P處.這時,一輛出租車由西向東勻速行駛,測得此車從A處行駛到B處所用的時間為4秒,且∠APO=60°,∠BPO=45°.
超速行駛是引發交通事故的主要原因.上周末,小明和三位同學嘗試用自己所學的知識檢測車速,如圖,觀測點設在到縣城城南大道的距離為100米的點P處.這時,一輛出租車由西向東勻速行駛,測得此車從A處行駛到B處所用的時間為4秒,且∠APO=60°,∠BPO=45°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
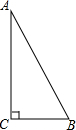 如圖,在Rt△ABC中,AC=12mm,AB=13mm,在頂點A處有一只螞蟻,以每秒4mm的速度沿AC方向爬行;在頂點B處有一只蝸牛,以每秒1mm的速度沿BC方向爬行.當它們同時出發爬行2秒后相距多少mm?
如圖,在Rt△ABC中,AC=12mm,AB=13mm,在頂點A處有一只螞蟻,以每秒4mm的速度沿AC方向爬行;在頂點B處有一只蝸牛,以每秒1mm的速度沿BC方向爬行.當它們同時出發爬行2秒后相距多少mm?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 某種幼苗在一定條件下的移植成活率 | |
| B. | 某種柑橘在某運輸過程中的損壞率 | |
| C. | 某運動員在某種條件下“射出9環以上”的概率 | |
| D. | 投擲一枚均勻的骰子,朝上一面為偶數的概率 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com