【題目】設計建造一條道路，路基的橫斷面為梯形ABCD，如圖（單位：米）．設路基高為h，兩側的坡角分別為
和
，已知h=2，
，
，
．
（1）求路基底部AB的寬；
（2）修筑這樣的路基1000米，需要多少土石方？
【答案】(1)16米；（2）26000立方米.
【解析】
（1）分別過D、C作下底AB的垂線，設垂足為E、F．在Rt△ADE和Rt△BCF中，可根據h的長以及坡角的度數或坡比的值，求出AE、BF的長，進而可求得AB的值．
（2）根據（1）得出的梯形下底寬，可求出梯形的面積，進而可求出需要多少土石方．
（1）過D作DE⊥AB于E，過C作CF⊥AB于F．
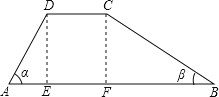
Rt△ADE中，∠α=45°，DE=h=2，
∴AE=DE=h=2．
Rt△BCF中，tanβ=
，CF=h=2，
∴BF=2CF=4．
故AB=AE+EF+BF=AE+CD+BF=2+10+4=16．
（2）S梯形ABCD=（AB+CD）h=×（10+16）×2=26．
因此所需的土石方數是：26×1000=26000（立方米）．
特高級教師點撥系列答案科目：初中數學 來源： 題型：
【題目】如圖，等邊
，點
為射線
上一點，延長
至點
，使得
，聯結
并延長交射線
于點
。
（1）當點在邊上時，如圖1，若
，則
（2）當點在邊上時，如圖2，若
，則（1）的結論還成立嗎？若成立，請證明；若不成立，寫出
與
的數量關系并證明。
（3）當點在邊的延長線上時，則（1）的結論還成立嗎？若成立，請證明；若不成立，寫出與的數量關系并證明。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數
的圖象與反比例函數
的圖象交于點
﹙
，
﹚，
﹙
，
﹚，交
軸于點
，交
軸于點
．
求反比例函數和一次函數的表達式；
連接
，
，求
的面積；
根據圖象寫出使一次函數的值小于反比例函數的值的的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義感知：我們把頂點關于
軸對稱，且交于軸上同一點的兩條拋物線叫做“孿生拋物線”，該點叫“孿生拋物線”的“共點”．如圖所示的拋物線
與
是一對“孿生拋物線”，其“共點”為點
．
初步運用：
判斷下列論斷是否正確？正確的在題后橫線上打“√”，錯誤的則打“
”：
①“孿生拋物線”的“共點”不能分布在
軸上．________
②“孿生拋物線”
與
的“共點”坐標為
．________
填空：拋物線
的“孿生拋物線”的解析式為________．
延伸拓展：在平面直角坐標系中，記“孿生拋物線”的兩頂點分別為
，
，且
，其“共點”與，，
三點恰好構成一個面積為
的菱形，試求該“孿生拋物線”的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，小明在一次高爾夫球爭霸賽中從山坡上的點
打出一球向球洞
飛去，球的飛行路線為拋物線，如果不考慮空氣阻力，當球達到最大鉛垂高度
時，球移動的水平距離為
．已知山坡
與水平方向
的夾角為
，，兩點相距
．
求出點的坐標；
求拋物線解析式．并判斷小明這一桿能否把高爾夫球從點直接打入球洞？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，二次函數
的圖象經過點
和
，下列關于此二次函數的敘述，正確的是（ ）
A. 當
時，
的值小于
B. 當
時，的值大于
C. 當
時，的值等于
D. 當
時，的值大于
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知
，則在下列條件：①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任選一個能判定△ABC≌△ABD的是( )
A. ①②③④ B. ②③④ C. ①③④ D. ①②③
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知二次函數
的圖象過點
和點
，對稱軸為直線
．
求該二次函數的關系式和頂點坐標；
結合圖象，解答下列問題：
①當
時，求函數
的取值范圍．
②當
時，求
的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】冬天，小芳給自己家剛剛裝滿水且顯示溫度為
的太陽能熱水器里的水加熱.她每過一段時間去觀察一下顯示溫度，并記錄如下：
時間（分鐘） | 0 | 5 | 10 | 15 | 20 | …… |
顯示溫度（ | 16 | 17 | 18 | 19 | 20 | …… |
（1）請直接寫出顯示溫度（
）與加熱時間（
）之間的函數關系式；
（2）如果她給熱水器設定的最高溫度為
，問：要加熱多長時間才能達到設定的最高溫度？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
