
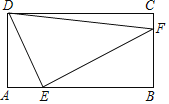
【題目】如圖,點E是矩形ABCD邊AB上一動點(不與點B重合),過點E作EF⊥DE交BC于點F,連接DF,已知AB=4cm,AD=2cm,設A,E兩點間的距離為xcm,△DEF面積為ycm2.
小明根據學習函數的經驗,對函數y隨自變量x的變化而變化的規律進行了探究.
下面是小明的探究過程,請補充完整:
(1)確定自變量x的取值范圍是 ;
(2)通過取點、畫圖、測量、分析,得到了x與y的幾組值,如表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y/cm2 | 4.0 | 3.7 | 3.9 | 3.8 | 3.3 | 2.0 | … |
(說明:補全表格時相關數值保留一位小數)
(3)建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;

(4)結合畫出的函數圖象,解決問題:當△DEF面積最大時,AE的長度為 cm.
【答案】(1)0≤x<4;(2)3.8,4.0;(3)見解析;(4)0,2.
【解析】
(1)利用點E在線段AB上,即可得出結論;
(2)先判斷出△ADE∽△BEF,得出![]() ,進而表示出BF=
,進而表示出BF=![]() ,再取x=1和x=2求出y的即可;
,再取x=1和x=2求出y的即可;
(3)利用畫函數圖象的方法即可得出結論;
(4)由圖象可知,即可得出結論.
(1)∵點E在AB上,
∴0≤x<4,
故答案為:0≤x<4;
(2)∵四邊形ABCD是矩形,
∴BC=AD=2,CD=AB=4,∠A=∠B=90°,
∴∠ADE+∠AED=90°,
∵EF⊥DE,
∴∠AED+∠BEF=90°,
∴∠ADE=∠BEF,
∵∠A=∠B=90°,
∴△ADE∽△BEF,
∴![]() ,
,
∵AE=x,
∴BE=AB﹣AE=4﹣x,
∴![]() ,
,
∴BF=![]() ,
,
當x=1時,BF=![]() ,
,
∴CF=BC﹣BF=2﹣![]() =
=![]() ,
,
y=S矩形ABCD﹣S△ADE﹣S△BEF﹣S△CDF=8﹣![]() ×2×1﹣
×2×1﹣![]() ×3×
×3×![]() ﹣
﹣![]() ×4×
×4×![]() =3.75≈3.8,
=3.75≈3.8,
當x=2時,BF=2,
∴CF=BC﹣BF=0,此時,點F和點C重合,
y=S矩形ABCD﹣S△ADE﹣S△BEF=8﹣![]() ×2×2﹣
×2×2﹣![]() ×2×2=4.0
×2×2=4.0
故答案為:3.8,4.0
(3)描點,連線,畫出如圖所示的圖象,

(4)由圖象可知,當x=0或2時,△DEF面積最大,
即:當△DEF面積最大時,AE=0或2,
故答案為0,2.


 每課必練系列答案
每課必練系列答案科目:初中數學 來源: 題型:
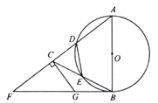
【題目】如圖,在![]() 中,
中,![]() .以
.以![]() 為直徑的
為直徑的![]() 與
與![]() 交于點
交于點![]() ,與
,與![]() 交于點
交于點![]() ,點
,點![]() 在邊
在邊![]() 的延長線上,且
的延長線上,且![]() .
.
(1)試說明![]() 是
是![]() 的切線;
的切線;
(2)過點![]() 作
作![]() ,垂足為
,垂足為![]() .若
.若![]() ,
,![]() ,求
,求![]() 的半徑;
的半徑;
(3)連接![]() ,設
,設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=8,BC=6,以邊AB的中點O為圓心,作半圓與AC相切于點M,P、Q分別是邊BC和半圓上的動點,連接PQ,則PQ長的最小值是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
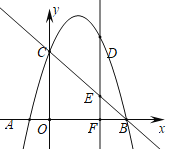
【題目】如圖,已知拋物線![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C.
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C.
(1)直接寫出點A、B、C的坐標;
(2)在拋物線的對稱軸上存在一點P,使得PA+PC的值最小,求此時點P的坐標;
(3)點D是第一象限內拋物線上的一個動點(與點C、B不重合)過點D作DF⊥x軸于點F,交直線BC于點E,連接BD,直線BC把△BDF的面積分成兩部分,使![]() ,請求出點D的坐標;
,請求出點D的坐標;
(4)若M為拋物線對稱軸上一動點,使得△MBC為直角三角形,請直接寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四川是聞名天下的“熊貓之鄉”,每年到大熊貓基地游玩的游客絡繹不絕,大學生小張加入創業項目,項目幫助她在基地附近租店賣創意熊貓紀念品.已知某款熊貓紀念物成本為30元/件,當售價為45元/件時,每天銷售250件,售價每上漲1元,銷量下降10件.
(1)求每天的銷售量y(件)與銷售單價x(元)之間的函數關系式;
(2)若每天該熊貓紀念物的銷售量不低于240件的情況下,當銷售單價為多少元時,每天獲取的利潤最大?最大利潤是多少?
(3)小張決定從這款紀念品每天的銷售利潤中捐出150元給希望工程,為了保證捐款后這款紀念品每天剩余利潤不低于3600元,試確定該熊貓紀念物銷售單價的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
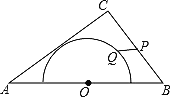
【題目】如圖,在△ABC中,AB=10,AC=8,BC=6,以邊AB的中點O為圓心,作半圓與AC相切,點P、Q分別是邊BC和半圓上的動點,連接PQ,則PQ長的最大值與最小值的和是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
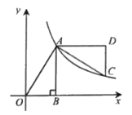
【題目】如圖,雙曲線![]() 上的一點
上的一點![]() ,其中
,其中![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,連接
,連接![]() .
.
(1)已知![]() 的面積是
的面積是![]() ,求
,求![]() 的值;
的值;
(2)將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,且點
,且點![]() 的對應點
的對應點![]() 恰好落在該雙曲線上,求
恰好落在該雙曲線上,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com