
【題目】參照學習函數的過程與方法,探究函數![]()
![]() 的圖象與性質.因為
的圖象與性質.因為![]() ,即
,即![]() ,所以我們對比函數
,所以我們對比函數![]() 來探究.
來探究.
列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描點:在平面直角坐標系中,以自變量![]() 的取值為橫坐標,以
的取值為橫坐標,以![]() 相應的函數值為縱坐標,描出相應的點,如圖所示:
相應的函數值為縱坐標,描出相應的點,如圖所示:
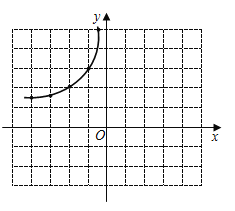
(1)請補全函數圖象;
(2)觀察圖象并分析表格,回答下列問題:
①當![]() 時,
時,![]() 隨
隨![]() 的增大而_________;(填“增大”或“減小”)
的增大而_________;(填“增大”或“減小”)
②![]() 的圖象是由
的圖象是由![]() 的圖象向________平移________個單位而得到;
的圖象向________平移________個單位而得到;
③圖象關于點_________中心對稱.(填點的坐標)
(3)結合函數圖象,當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見詳解;(2)增大,上,1,(0,1);(3)﹣1<x<0或x>1
【解析】
(1)用光滑曲線順次連接即可;
(2)利用圖象法即可解決問題;
(3)聯立方程求出點A、B的坐標,由此即可解決問題.
解:(1)函數圖象如圖所示:
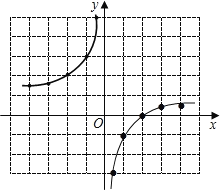
(2)①當x<0時,y隨x的增大而增大;
②![]() 的圖象是由y=
的圖象是由y=![]() 的圖象向上平移1個單位而得到;
的圖象向上平移1個單位而得到;
③圖象關于點(0,1)中心對稱.
故答案為:增大,上,1,(0,1);
(3)根據題意得:![]() =﹣2x+1,解得:x=±1,
=﹣2x+1,解得:x=±1,
當x=1時,y=﹣2x+1=﹣1,
當x=﹣1時,y=﹣2x+1=3,
∴交點為(1,﹣1),(﹣1,3),
∴當![]() >﹣2x+1時,求x的取值范圍為﹣1<x<0或x>1.
>﹣2x+1時,求x的取值范圍為﹣1<x<0或x>1.


科目:初中數學 來源: 題型:
【題目】宣和中學圖書館今日購進甲、乙兩種圖書,每本甲種圖書的進價比每本乙種圖書的進價高20元,花780元購進甲種圖書的數量與花540元購進乙種圖書的數量相同.
(1)求甲、乙兩種圖書每本的進價分別是多少元;
(2)宣和中學購進甲、乙兩種圖書共70本,總購書費用不超過3950元,則最多購進甲種圖書多少本.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】著名數學教育家波利亞曾說:“對一個數學問題,改變它的形式,變換它的結構,直到發現有價值的東西,這是數學解題的一個重要原則.”
閱讀下列兩則材料,回答問題
材料一:平方運算和開方運算是互逆運算,如:a2±2ab+b2=(a±b)2,那么![]() =|a±b|,那么如何將雙重二次根式
=|a±b|,那么如何將雙重二次根式![]() (a>0,b>0,a±2
(a>0,b>0,a±2![]() >0)化簡呢?如能找到兩個數m,n(m>0,n>0),使得(
>0)化簡呢?如能找到兩個數m,n(m>0,n>0),使得(![]() 2+(
2+(![]() )2=a即m+n=a,且使
)2=a即m+n=a,且使![]() 即mn=b,那么a±2
即mn=b,那么a±2![]() =(
=(![]() )2+(
)2+(![]() )2±2
)2±2![]() =(
=(![]() 2
2
∴![]() =
=![]() =
=![]() |,雙重二次根式得以化簡.
|,雙重二次根式得以化簡.
例如化簡:![]() .∵3=1+2且2=1×2,∴3+2
.∵3=1+2且2=1×2,∴3+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() ,
,
∴![]() =
=![]() =1+
=1+![]() .
.
材料二:在直角坐標系xoy中,對于點P(x,y)和Q(x,y′)出如下定義:若y′=![]() ,則稱點Q為點P的“橫負縱變點”例如,點(3,2)的“橫負縱變點”為(3,2),點(﹣2,5)的“橫負縱變點”為(﹣2,﹣5)
,則稱點Q為點P的“橫負縱變點”例如,點(3,2)的“橫負縱變點”為(3,2),點(﹣2,5)的“橫負縱變點”為(﹣2,﹣5)
問題:
(1)請直接寫出點(﹣3![]() ,﹣2)的“橫負縱變點”為 ;化簡
,﹣2)的“橫負縱變點”為 ;化簡![]() = ;
= ;
(2)點M為一次函數y=﹣x+1圖象上的點,M′為點M的橫負縱變點,已知N(1,1),若M′N=![]() ,求點M的坐標;
,求點M的坐標;
(3)已知b為常數且1≤b≤2,點P在函數y=﹣x2+16(![]() +)(
+)(![]() ﹣7≤x≤a)的圖象上,其“橫負縱變點”的縱坐標y′的取值范圍是﹣32<y′≤32,若a為偶數,求a的值.
﹣7≤x≤a)的圖象上,其“橫負縱變點”的縱坐標y′的取值范圍是﹣32<y′≤32,若a為偶數,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2﹣2ax﹣2的圖象(記為拋物線C1)頂點為M,直線l:y=2x﹣a與x軸,y軸分別交于A,B.
(1)對于拋物線C1,以下結論正確的是 ;
①對稱軸是:直線x=1;②頂點坐標(1,﹣a﹣2);③拋物線一定經過兩個定點.
(2)當a>0時,設△ABM的面積為S,求S與a的函數關系;
(3)將二次函數y=ax2﹣2ax﹣2的圖象C1繞點P(t,﹣2)旋轉180°得到二次函數的圖象(記為拋物線C2),頂點為N.
①當﹣2≤x≤1時,旋轉前后的兩個二次函數y的值都會隨x的增大而減小,求t的取值范圍;
②當a=1時,點Q是拋物線C1上的一點,點Q在拋物線C2上的對應點為Q',試探究四邊形QMQ'N能否為正方形?若能,求出t的值,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】不覽夜景,未到重慶山城夜景,早在清乾隆時期就已有名氣,被時任巴縣知縣王爾鑒,列為巴渝十二景之一在朝天門碼頭坐船游兩江(即長江、嘉陵江),是游重慶賞夜景的一個經典項目.一艘輪船從朝天門碼頭出發勻速行駛,![]() 小時后一快艇也從朝天門碼頭出發沿同一線路勻速行駛,當快艇先到達目的地后立刻按原速返回并在途中與輪船第二次相遇.設輪船行駛的時間為
小時后一快艇也從朝天門碼頭出發沿同一線路勻速行駛,當快艇先到達目的地后立刻按原速返回并在途中與輪船第二次相遇.設輪船行駛的時間為![]()
![]() ,快艇和輪船之間的距離為
,快艇和輪船之間的距離為![]() ,
,![]() 與
與![]() 的函數關系式如圖所示,則快艇與輪船第二次相遇時到朝天門碼頭的距離為_____千米.
的函數關系式如圖所示,則快艇與輪船第二次相遇時到朝天門碼頭的距離為_____千米.
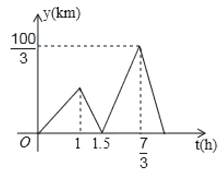
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數 y=ax2+bx+c 的圖象與 x 軸的交點的橫坐標分別為-1,3,則:
①ac<0;②2a+b=0;③4a+2b+c>0;④對于任意 x 均有 ax2+bx≥a+b,其中結論正確的個數有( )
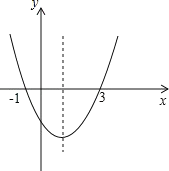
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某校綜合實踐活動小組的同學欲測量公園內一棵樹DE的高度,他們在這棵樹的正前方一座樓亭前的臺階上A點處測得樹頂端D的仰角為30°,朝著這棵樹的方向走到臺階下的點C處,測得樹頂端D的仰角為60°.已知A點的高度AB為3米,臺階AC的坡度為1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三點在同一條直線上.請根據以上條件求出樹DE的高度.
),且B、C、E三點在同一條直線上.請根據以上條件求出樹DE的高度.

查看答案和解析>>
科目:初中數學 來源: 題型:
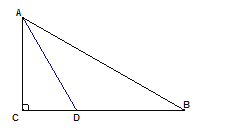
【題目】已知,如圖,在Rt△ABC中,∠C=90,∠BAC的角平分線AD交BC邊于D.
(1)以AB邊上一點O為圓心作⊙O,使它過A,D兩點(不寫作法,保留作圖痕跡),再判斷直線BC與⊙O的位置關系,并說明理由;
(2)若(1)中的⊙O與AB邊的另一個交點為E,AB=3![]() ,BD=3,求線段BD、BE與劣弧DE所圍成的圖形面積.(結果保留根號和
,BD=3,求線段BD、BE與劣弧DE所圍成的圖形面積.(結果保留根號和![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,菱形ABCD中,∠B=60°,動點P以每秒1個單位的速度自點A出發沿線段AB運動到點B,同時動點Q以每秒2個單位的速度自點B出發沿折線B﹣C﹣D運動到點D.圖2是點P、Q運動時,△BPQ的面積S隨時間t變化關系圖象,則a的值是( )
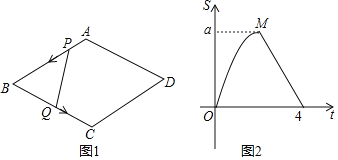
A.2B.2.5C.3D.2![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com