
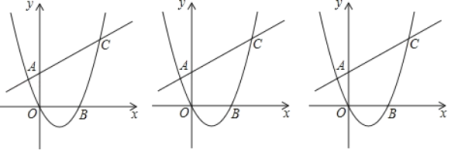
【題目】如圖,二次函數y=ax2﹣4ax(a≠0)的圖象與直線y=kx+3交于點A(﹣1,![]() )、點C兩點.
)、點C兩點.
(1)求a,k的值;
(2)點P在第一象限的拋物線上,其橫坐標為t,連接PC、PA,設△PCA的面積為S,求S關于t的函數關系式:(直接寫出t的取值范圍)
(3)在(2)的條件下,作CE⊥x軸于E,點P直線y=kx+3下方時,連接OP、BC交于D,連接ED,當∠ODE=90°時,求t和S的值.
【答案】(1)a=![]() ,k=
,k=![]() ;(2)S=
;(2)S=![]() ,(4<t<6)或
,(4<t<6)或![]() ,( t>6); (3)解得t=5,S=
,( t>6); (3)解得t=5,S=![]() .
.
【解析】
(1)將A(-1,![]() )代入二次函數y=ax2-4ax(a≠0)與直線y=kx+3中,可得a,k的值;
)代入二次函數y=ax2-4ax(a≠0)與直線y=kx+3中,可得a,k的值;
(2)分P點再BC中,與BC右側兩種情況討論計算可得答案;
(3)由∠ODE=90°,![]() =-1,可得方程D點坐標,計算可得t,s的值.
=-1,可得方程D點坐標,計算可得t,s的值.
解:(1)將A(-1,![]() )代入二次函數y=ax2-4ax(a≠0)與直線y=kx+3;
)代入二次函數y=ax2-4ax(a≠0)與直線y=kx+3;
可得:a=![]() ,k=
,k=![]() ;
;
(2)易得B點坐標(4,0),聯立二次函數y=![]() ,與一次函數y=
,與一次函數y=![]() ,可得
,可得
C點坐標(6,6),
如圖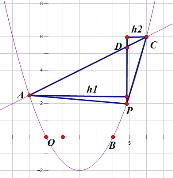
當P點再BC中間時候,橫坐標為t,(4<t<6),可得P(t,![]() ),D(t,
),D(t,![]() )
)
![]()
![]() =
=![]() -(
-(![]() )=
)=![]() ,
,
過點P做AC的垂線垂足為D,過A點做DP的垂線,設垂線長為![]() ,過C點做DP的垂線, 垂線長為
,過C點做DP的垂線, 垂線長為![]() ,可得
,可得![]() =
=![]() =7,
=7,
![]()
![]() =
=![]()
![]()
![]() (
(![]() )=
)=![]()
![]() (
(![]() )
)![]() 7=
7=![]() ,(4<t<6);
,(4<t<6);
如圖,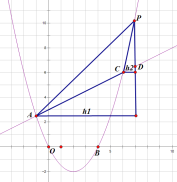
同理,當P點再C右側時,即t>6時,
同理過點PD⊥x軸,交AC與D點,過點C做垂線垂直PD,垂線長為![]() ,過A點做垂線垂直PD,垂線長為
,過A點做垂線垂直PD,垂線長為![]() ,易得
,易得![]() =
=![]() =7,
=7,![]() =
=![]() -(
-(![]() )=
)=![]() ,
,
易得:![]() =
=![]()
![]()
![]() (
(![]() )=
)=![]() ,( t>6)
,( t>6)
(3)如圖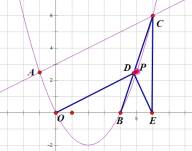
易得:E點坐標(6,0),B點(4,0),
可得BC直線的方程:y=3x-12,
設D點坐標為(x,3x-12),4<x<6,由∠ODE=90°,
可得![]() =-1,可得,
=-1,可得,![]() ,
,
化簡得:![]() ;
;
可得:![]() =3(舍去),
=3(舍去),![]() =
=![]() ,
,
可得:D點坐標(![]() ,
,![]() )
)
可得OD的方程為y=![]() ,
,
聯立OD與二次函數的方程可得: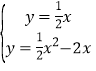
可得x=5,即t=5,
代入![]() =
=![]() ,可得S=
,可得S=![]() ,
,
故答案:t=5,s=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在一個木制的棱長為3的正方體的表面涂上顏色,將它的棱三等分,然后從等分點把正方體鋸開,得到27個棱長為l的小正方體,將這些小正方體充分混合后,裝入口袋,從這個口袋中任意取出一個小正方體,則這個小正方體的表面恰好涂有兩面顏色的概率是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O是梯形ABCD的內切圓,AB∥DC,E、M、F、N分別是邊AB、BC、CD、DA上的切點.
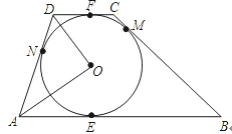
(1)求證:AB+CD=AD+BC
(2)求∠AOD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一個可以自由轉動的轉盤中,指針位置固定,三個扇形的面積都相等,且分別標有數字1,2,3.

(1)小明轉動轉盤一次,當轉盤停止轉動時,指針所指扇形中的數字是奇數的概率為________;
(2)小明先轉動轉盤一次,當轉盤停止轉動時,記錄下指針所指扇形中的數字;接著再轉動轉盤一次,當轉盤停止轉動時,再次記錄下指針所指扇形中的數字,求這兩個數字之和是3的倍數的概率(用畫樹狀圖或列表等方法求解)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一圓內接正八邊形ABCDEFGH,若△ADE的面積為8,則正八邊形ABCDEFGH的面積為( )
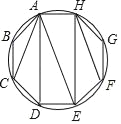
A. 32 B. 40 C. 24 D. 30
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有甲、乙兩個不透明的布袋,甲袋中裝有3個完全相同的小球,分別標有數字1,2,3;乙袋中裝有3個完全相同的小球,分別標有數字﹣1,﹣2,﹣3,現從甲袋中隨機摸出一個小球,將標有的數字記錄為x,再從乙袋中隨機摸出一個小球,將標有的數字記錄為y,確定點M的坐標為(x,y).
(1)用樹狀圖或列表法列舉點M所有可能的坐標;
(2)求點M(x,y)在反比例函數y=![]() 的圖象上的概率.
的圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在兩個全等的等腰直角三角形ABC和EDC中,∠ACB=∠ECD=90°,點A與點E重合,點D與點B重合.現△ABC不動,把△EDC繞點C按順時針方向旋轉,旋轉角為α(0°<α<90°).
(1)如圖②,AB與CE交于點F,ED與AB,BC分別交于點M,H.求證:CF=CH;
(2)如圖③,當α=45°時,試判斷四邊形ACDM的形狀,并說明理由;
(3)如圖②,在△EDC繞點C旋轉的過程中,連結BD,當旋轉角α的度數為多少時,△BDH是等腰三角形?



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,AB、AC是圓O的兩條弦,AB=AC,過圓心O作OH⊥AC于點H.

(1)如圖1,求證:∠B=∠C;
(2)如圖2,當H、O、B三點在一條直線上時,求∠BAC的度數;
(3)如圖3,在(2)的條件下,點E為劣弧BC上一點,CE=6,CH=7,連接BC、OE交于點D,求BE的長和![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com