
【題目】已知拋物線![]() .
.
(1)若該拋物線與x軸有公共點,求c的取值范圍;
(Ⅱ)設該拋物線與直線![]() 交于M,N兩點,若
交于M,N兩點,若![]() ,求C的值;
,求C的值;
(Ⅲ)點P,點Q是拋物線上位于第一象限的不同兩點,![]() 都垂直于x軸,垂足分別為A,B,若
都垂直于x軸,垂足分別為A,B,若![]() ,求c的取值范圍.
,求c的取值范圍.
【答案】(I)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)c的取值范圍是
;(Ⅲ)c的取值范圍是![]()
【解析】
(1) 拋物線與x軸有公共點,則判別式為非負數,列不等式求解即可;
(2)求出二次函數與直線的交點,并根據勾股定理求出MN的長度,列方程即可求解;
(3)由![]() 可知,P,Q兩點的坐標特點,設坐標得到設點P的坐標為
可知,P,Q兩點的坐標特點,設坐標得到設點P的坐標為![]() ,則點Q的坐標為
,則點Q的坐標為![]() ,代入二次函數,得到n,m的關系,則只需保證該方程有正根即可求解.
,代入二次函數,得到n,m的關系,則只需保證該方程有正根即可求解.
解:(I)∵拋物線![]() 與x軸有交點,
與x軸有交點,
∴一元二次方程![]() 有實根。
有實根。
![]() ,即
,即![]() .解得
.解得![]()
(Ⅱ)根據題意,設![]()
由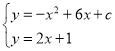 ,消去y,得
,消去y,得![]() ①.
①.
由![]() ,得
,得![]() .
.
∴方程①的解為![]()
![]()
![]() ,解得
,解得![]()
(Ⅲ)設點P的坐標為![]() ,則點Q的坐標為
,則點Q的坐標為![]() ,且
,且![]() ,
,
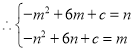 ,兩式相減,得
,兩式相減,得![]() ,即
,即![]()
![]() ,即
,即![]()
![]() ,其中
,其中![]()
由![]() ,即
,即![]() ,得
,得![]() .
.
當![]() 時,
時,![]() ,不合題意。
,不合題意。
又![]() ,得
,得![]() .
.
∴c的取值范圍是![]()


科目:初中數學 來源: 題型:
【題目】拋物線![]() 的頂點為
的頂點為![]() ,與直線
,與直線![]() 相交于點
相交于點![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() .
.
(Ⅰ)若拋物線![]() 經過原點,求
經過原點,求![]() 的值;
的值;
(Ⅱ)是否存在![]() 的值,使得點
的值,使得點![]() 到
到![]() 軸距離等于點
軸距離等于點![]() 到直線
到直線![]() 距離的一半,若存在,請直接寫出
距離的一半,若存在,請直接寫出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(Ⅲ)將![]() 的函數圖象記為圖象
的函數圖象記為圖象![]() ,圖象
,圖象![]() 關于直線
關于直線![]() 的對稱圖象記為圖象
的對稱圖象記為圖象![]() ,圖象
,圖象![]() 與圖象
與圖象![]() 組合成的圖象記為
組合成的圖象記為![]() .
.
①當![]() 與
與![]() 軸恰好有三個交點時,求
軸恰好有三個交點時,求![]() 的值:
的值:
②當![]() 為等邊三角形時,直接寫出
為等邊三角形時,直接寫出![]() 所對應的函數值小于0時,自變量
所對應的函數值小于0時,自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() (b,c為常數)與x軸交于點
(b,c為常數)與x軸交于點![]() 和
和![]() ,與y軸交于點A,點E為拋物線頂點。
,與y軸交于點A,點E為拋物線頂點。
(Ⅰ)當![]() 時,求點A,點E的坐標;
時,求點A,點E的坐標;
(Ⅱ)若頂點E在直線![]() 上,當點A位置最高時,求拋物線的解析式;
上,當點A位置最高時,求拋物線的解析式;
(Ⅲ)若![]() ,當
,當![]() 滿足
滿足![]() 值最小時,求b的值。
值最小時,求b的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】陽春三月,龍泉驛區的桃花又開了,小明乘坐地鐵到龍泉看桃花,計劃在龍平路地鐵口下車,如圖是龍平路地鐵口的平面圖,其有A、B、C、D四個出入口,小明任選一個出口下車出站,賞花結束后,任選一個入口入站乘車.
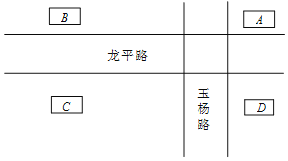
(1)小明從出站到入站共有多少種可能的結果?請用樹形圖或列表說明;
(2)求出小明從龍平路同一側出入站的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組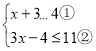
請結合題意填空,完成本題的解答:
(I)解不等式①,得_____________________;
(Ⅱ)解不等式②,得_________________________;
(Ⅲ)把不等式①和②的解集在數軸上表示出來:

(IV)原不等式組的解集為____________________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
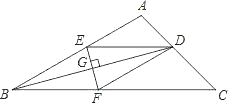
【題目】如圖,在 ABC 中,BD 平分ABC 交 AC 于 D ,EF 垂直平分 BD ,分別交 AB, BC, BD于 E, F , G ,連接 DE, DF 。
(1)求證:四邊形 BEDF 為菱形;
(2)若ABC 30, C 45, DE 4 ,求CF 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組 ;請結合題意填空,完成本題的解答.
;請結合題意填空,完成本題的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在數軸上表示出來:
![]()
(Ⅳ)原不等式組的解集為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
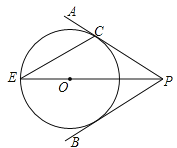
【題目】如圖,點O在∠APB的平分線上,⊙O與PA相切于點C.
(1)求證:直線PB與⊙O相切;
(2)PO的延長線與⊙O交于點E.若⊙O的半徑為3,PC=4.求弦CE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com