
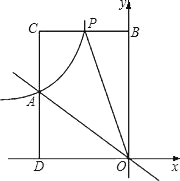
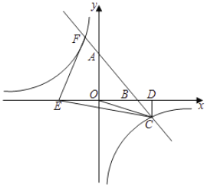
【題目】如圖所示,正比例函數y=kx與反比例函數![]() 的圖象交于點A(﹣3,2).
的圖象交于點A(﹣3,2).
(1)試確定上述正比例函數與反比例函數的解析式;
(2)根據圖象回答,在第二象限內,當x取何值時,反比例函數的值大于正比例函數的值?
(3)P(m,n)是反比例函數圖象上的一動點,其中﹣3<m<0,過點P作直線PB∥x軸,交y軸于點B,過點A作直線AD∥y軸,交x軸于點D,交直線PB于點C.當四邊形OACP的面積為6時,請判斷線段BP與CP的大小關系,并說明理由.
【答案】(1)正比例函數與反比例函數的解析式分別是y=﹣![]() x,y=﹣
x,y=﹣![]() .(2)﹣3<x<0;(3)線段BP與CP的大小關系是BP=CP.
.(2)﹣3<x<0;(3)線段BP與CP的大小關系是BP=CP.
【解析】
(1)把A的坐標代入解析式求出k、m即可;
(2)畫出圖象,根據圖象,當x取相同的數時y的值即可求出答案;
(3)求出mn的值,根據三角形的面積公式得到3n-![]() ×3×2-
×3×2-![]() ×(-mn)=6,求出m、n的值,求出BP、CP的值即可.
×(-mn)=6,求出m、n的值,求出BP、CP的值即可.
(1)把A(﹣3,2)代入y=kx得:2=﹣3k,
解得:k=﹣![]() ,
,
∴y=﹣![]() x,
x,
代入y=![]() 得:m=﹣6,
得:m=﹣6,
∴y=﹣![]() ,
,
答:正比例函數與反比例函數的解析式分別是y=﹣![]() x,y=﹣
x,y=﹣![]() .
.
(2)∵A(﹣3,2),
由圖象可知:當﹣3<x<0時,在第二象限內,反比例函數的值大于正比例函數的值.
(3)答:線段BP與CP的大小關系是BP=CP,
理由是:∵P(m,n)在y=﹣![]() 上,
上,
∴mn=﹣6,
∵DO=3,AD=2,OB=n,BP=﹣m,CP=3﹣PB,DC=n,
四邊形OACP的面積為6,
∴S矩形CDOB﹣S△ADO﹣S△OBP=6,
3n﹣![]() ×3×2﹣
×3×2﹣![]() ×(﹣mn)=6,
×(﹣mn)=6,
3n﹣3﹣![]() ×6=6,
×6=6,
3n=12,
解得:n=4,
∴m=﹣![]() ,
,
∴P(﹣![]() ,4),
,4),
∴PB=![]() ,CP=3﹣
,CP=3﹣![]() =
=![]() ,
,
∴BP=CP.


科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD,點E在BA延長線上,點F在BC上,且∠CDE=2∠ADF.
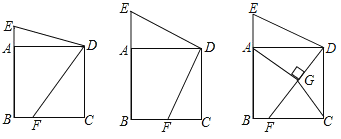
(1)求證:∠E=2∠CDF;
(2)若F是BC中點,求證:AE+DE=2AD;
(3)作AG⊥DF于點G,連CG.當CG取最小值時,直接寫出AE:AB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四邊形![]() 中,
中,![]() ,垂足為點
,垂足為點![]() ,
,![]() .
.
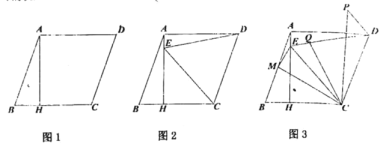
(1)如圖1,求證:![]() ;
;
(2)如圖2,點![]() 為
為![]() 上一點,連接
上一點,連接![]() ,
,![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,如圖3,點![]() 為
為![]() 上一點,連接
上一點,連接![]() ,點
,點![]() 為
為![]() 的中點,分別連接
的中點,分別連接![]() ,
,![]() ,
,![]() +
+![]() =
=![]() =
=![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
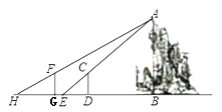
【題目】假山具有多方面的造景功能,與建筑、植物等組合成富于變化的景致.某公園有一座假山,小亮、小慧等同學想用一些測量工具和所學的幾何知識測量這座假山的高度來檢驗自己掌握知識和運用知識的能力,如圖,在陽光下,小亮站在水平地面的D處,此時小亮身高的影子頂端與假山的影子頂端E重合,這時小亮身高CD的影長DE=2米,一段時間后,小亮從D點沿BD的方向走了3.6米到達G處,此時小亮身高的影子頂端與假山的影子頂端H重合,這時小亮身高的影長GH=2.4米,已知小亮的身高CD=FG=1.5米,點G,E,D均在直線BH上,AB⊥BH,CD⊥BH,GF⊥BH,請你根據題中提供的相關信息,求出假山的高度AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于第二、四象限的
的圖象交于第二、四象限的![]() 、
、![]() 兩點,與
兩點,與![]() 、
、![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸于點
軸于點![]() ,連接
,連接![]() ,且
,且![]() 的面積為3,作點
的面積為3,作點![]() 關于
關于![]() 軸對稱點
軸對稱點![]() .
.
(1)求一次函數和反比例函數的解析式;
(2)連接![]() 、
、![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
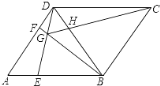
【題目】如圖,在菱形ABCD中,tanA= ![]() ,點E、F分別是AB、AD上任意的點(不與端點重合),且AE=DF,連接BF與DE相交于點G,連接CG與BD相交于點H,給出如下幾個結論:(1)△AED≌△DFB;(2)CG與BD一定不垂直;(3)∠BGE的大小為定值;(4)S四邊形BCDG=
,點E、F分別是AB、AD上任意的點(不與端點重合),且AE=DF,連接BF與DE相交于點G,連接CG與BD相交于點H,給出如下幾個結論:(1)△AED≌△DFB;(2)CG與BD一定不垂直;(3)∠BGE的大小為定值;(4)S四邊形BCDG= ![]() CG2;其中正確結論的序號為________.
CG2;其中正確結論的序號為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點O是邊AC上一個動點,過O作直線MN∥BC.設MN交∠ACB的平分線于點E,交∠ACB的外角平分線于點F.
(1)求證:OE=OF;
(2)若CE=8,CF=6,求OC的長;
(3)當點O在邊AC上運動到什么位置時,四邊形AECF是矩形?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,對角線AC、BD相交于點O,下列條件不能判定這個四邊形是平行四邊形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售一批名牌襯衫,平均每天可售出20件,每件盈利80元.為了擴大銷售、盡快減少庫存,商場決定采取適當的降價措施.經調查發現,如果每件襯衫每降價5元,商場平均每天就能多售出2件.請解答下列問題:
(1)當每件襯衫降價30元時,求商場每天銷售該襯衫所獲得的總利潤.
(2)當該襯衫每件降價多少元時,商場銷售該襯衫每天所獲得的利潤為1680元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com