
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于第二、四象限的
的圖象交于第二、四象限的![]() 、
、![]() 兩點,與
兩點,與![]() 、
、![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸于點
軸于點![]() ,連接
,連接![]() ,且
,且![]() 的面積為3,作點
的面積為3,作點![]() 關于
關于![]() 軸對稱點
軸對稱點![]() .
.
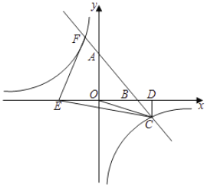
(1)求一次函數和反比例函數的解析式;
(2)連接![]() 、
、![]() ,求
,求![]() 的面積.
的面積.
【答案】(1)一次函數![]() ,反比例
,反比例![]() ,(2)
,(2)![]() .
.
【解析】
(1)點C在反比例函數![]() 圖象上,且△OCD的面積為3,并且圖象在二、四象限,可求出
圖象上,且△OCD的面積為3,并且圖象在二、四象限,可求出![]() 的值,確定反比例函數的關系式,再確定點C的坐標,用A、C的坐標用待定系數法可確定一次函數
的值,確定反比例函數的關系式,再確定點C的坐標,用A、C的坐標用待定系數法可確定一次函數![]() 的關系式, (2)利用一次函數
的關系式, (2)利用一次函數![]() 的關系式可求出于坐標軸的交點坐標,與反比例函數關系式聯立可求出F點坐標,利用對稱可求出點E坐標,最后由三角形的面積公式求出結果.
的關系式可求出于坐標軸的交點坐標,與反比例函數關系式聯立可求出F點坐標,利用對稱可求出點E坐標,最后由三角形的面積公式求出結果.
解:(1)∵點C在反比例函數![]() 圖象上,且△OCD的面積為3,
圖象上,且△OCD的面積為3,
∴ ![]() , ∴
, ∴![]() ,
,
∵反比例函數的圖象在二、四象限, ∴![]() ,
,
∴反比例函數的解析式為![]() ,
,
把C![]() 代入為:
代入為:![]() 得,
得,![]() , ∴C
, ∴C![]() ,
,
把A(0,4),C(3,-2)代入一次函數![]() 得:
得:
![]() ,解得:
,解得:![]() , ∴一次函數的解析式為
, ∴一次函數的解析式為![]() .
.
答:一次函數和反比例函數的解析式分別為:![]() ,
,![]() .
.
(2)一次函數![]() 與
與![]() 軸的交點B(2,0).
軸的交點B(2,0).
∵點B關于y軸對稱點E, ∴點E(-2,0), ∴BE=2+2=4,
一次函數和反比例函數的解析式聯立得: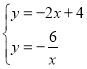 ,解得:
,解得:
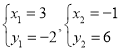 , ∴點
, ∴點![]() ,
,
∴![]() .
.
答:△EFC的面積為16.


科目:初中數學 來源: 題型:
【題目】某種電纜在空中架設時,兩端掛起的電纜下垂都近似成拋物線![]() 的形狀,現按操作要求,電纜最低點離水平地面不得小于6米.
的形狀,現按操作要求,電纜最低點離水平地面不得小于6米.
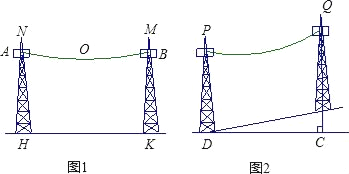
(1)如圖1,若水平距離間隔80米建造一個電纜塔柱,求此電纜塔柱用于固定電纜的位置離地面至少應有多少米的高度?
(2)如圖2,若在一個坡度為1:5的斜坡上,按水平距離間隔50米架設兩固定電纜的位置離地面高度為20米的塔柱.
①求這種情況下在豎直方向上,下垂的電纜與斜坡的最近距離為多少米?
②這種情況下,直接寫出下垂的電纜與地面的最近距離為多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不動,△ADE繞點A旋轉,連接BE,CD,F為BE的中點,連接AF.
(1)如圖①,當∠BAE=90°時,求證:CD=2AF;
(2)當∠BAE≠90°時,(1)的結論是否成立?請結合圖②說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“愛滿揚州”慈善一日捐活動中,學校團總支為了了解本校學生的捐款情況,隨機抽取了50名學生的捐款數進行了統計,并繪制成統計圖.

(1)這50名同學捐款的眾數為 元,中位數為 元;
(2)求這50名同學捐款的平均數;
(3)該校共有600名學生參與捐款,請估計該校學生的捐款總數.
查看答案和解析>>
科目:初中數學 來源: 題型:
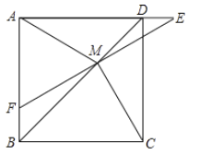
【題目】如圖,在正方形![]() 中,
中,![]() 是對角線
是對角線![]() 上的一點,點
上的一點,點![]() 在
在![]() 的延長線上,連接
的延長線上,連接![]() 、
、![]() 、
、![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() ,若
,若![]()
![]() ,
,![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正確的結論序號是( )
,其中正確的結論序號是( )
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
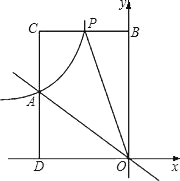
【題目】如圖所示,正比例函數y=kx與反比例函數![]() 的圖象交于點A(﹣3,2).
的圖象交于點A(﹣3,2).
(1)試確定上述正比例函數與反比例函數的解析式;
(2)根據圖象回答,在第二象限內,當x取何值時,反比例函數的值大于正比例函數的值?
(3)P(m,n)是反比例函數圖象上的一動點,其中﹣3<m<0,過點P作直線PB∥x軸,交y軸于點B,過點A作直線AD∥y軸,交x軸于點D,交直線PB于點C.當四邊形OACP的面積為6時,請判斷線段BP與CP的大小關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,M,N分別是邊AD,BC的中點,E,F分別是線段BM,CM的中點,當AB:AD=___________時,四邊形MENF是正方形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校獎勵給王偉和李麗上海世博園門票共兩張,其中一張為指定日門票,另一張為普通日門票。王偉和李麗分別轉動下圖的甲、乙兩個轉盤(轉盤甲被二等分、轉盤乙被三等分)確定指定日門票的歸屬,在兩個轉盤都停止轉動后,若指針所指的兩個數字之和為 偶數,則王偉獲得指定日門票;若指針所指的兩個數字之和為奇數,則李麗獲得指定日門票;若指針指向分隔線,則重新轉動。你認為這個方法公平嗎?請畫樹狀圖或列表,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com