
【題目】如圖,在ABCD中,AD=2AB,F是AD的中點,作CE⊥AB于E,在線段 AB上,連接EF、CF.則下列結論:①∠BCD=2∠DCF;②∠ECF=∠CEF;③S△BEC=2S△CEF;④∠DFE=3∠AEF,其中一定正確的是( )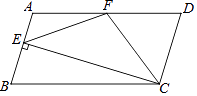
A.②④
B.①②④
C.①②③④
D.②③④
【答案】C
【解析】解:①∵F是AD的中點, ∴AF=FD,
∵在ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠BCD=2∠DCF,故①正確;
②延長EF,交CD延長線于M,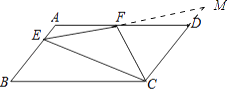
∵四邊形ABCD是平行四邊形,
∴AB∥CD,
∴∠A=∠MDF,
∵F為AD中點,
∴AF=FD,
在△AEF和△DFM中,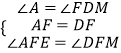 ,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FE,
∴∠ECF=∠CEF,故②正確;
③∵EF=FM,
∴S△EFC=S△CFM ,
∵MC>BE,
∴S△BEC<2S△EFC ,
故S△BEC=2S△CEF , 故③錯誤;
④設∠FEC=x,則∠FCE=x,
∴∠DCF=∠DFC=90°﹣x,
∴∠EFC=180°﹣2x,
∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x,
∵∠AEF=90°﹣x,
∴∠DFE=3∠AEF,故④正確,
故選:C.
【考點精析】解答此題的關鍵在于理解平行四邊形的性質的相關知識,掌握平行四邊形的對邊相等且平行;平行四邊形的對角相等,鄰角互補;平行四邊形的對角線互相平分.


科目:初中數學 來源: 題型:
【題目】我們把分子為1的分數叫做單位分數,如 ![]() ,
, ![]() ,
, ![]() ,…任何一個單位分數都可以拆分成兩個不同的單位分數的和,如
,…任何一個單位分數都可以拆分成兩個不同的單位分數的和,如 ![]() =
= ![]() +
+ ![]() ,
, ![]() =
= ![]() +
+ ![]() ,
, ![]() =
= ![]() +
+ ![]() ,…
,…
(1)根據對上述式子的觀察,你會發現 ![]() =
= ![]() +
+ ![]() ,則a= , b=;
,則a= , b=;
(2)進一步思考,單位分數 ![]() =
= ![]() +
+ ![]() (n是不小于2的正整數),則x=(用n的代數式表示)
(n是不小于2的正整數),則x=(用n的代數式表示)
(3)計算: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,把直線y=﹣2x+3沿y軸向上平移兩個單位長度后,得到的直線的函數關系式為( )
A. y=﹣2x+1 B. y=﹣2x﹣5 C. y=﹣2x+5 D. y=﹣2x+7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自行車公司調查陽光中學學生對其產品的了解情況,隨機抽取部分學生進行問卷,結果分“非常了解”、“比較了解”、“一般了解”、“不了解”四種類型,分別記為A、B、C、D.根據調查結果繪制了如下尚不完整的統計圖.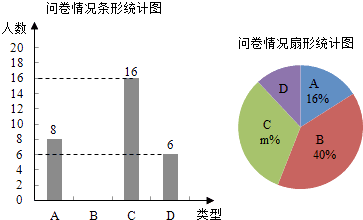
(1)本次問卷共隨機調查了名學生,扇形統計圖中m= .
(2)請根據數據信息補全條形統計圖.
(3)若該校有1000名學生,估計選擇“非常了解”、“比較了解”共約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場經營一批進價為2元一件的小商品,在銷售中發現此商品的日銷售單價![]() (元)與日銷售量
(元)與日銷售量![]() (件)之間有如下的一次函數關系:
(件)之間有如下的一次函數關系:

(1)求![]() 與
與![]() 的函數解析式;
的函數解析式;
(2)求日銷售額P(元)的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com