【題目】如圖，在□ABCD中，BE⊥AD于點E，BF⊥CD于點F，AC與BE、BF分別交于點G，H。
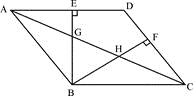
（1）求證：△BAE∽△BCF
（2）若BG＝BH，求證四邊形ABCD是菱形
【答案】（1）略
（2）略
【解析】
證明（1）∵BE⊥AD，BF⊥CD
∴∠BEA＝∠BFC＝90° ………………（1＇）
又ABCD是平行四邊形，
∴∠BAE＝∠BCF ……………………（2＇）
∴△BAE∽△BCF …………………………………………（3＇）
（2）∵△BAE∽△BCF
∴∠1＝∠2 ……………………………………………（4＇）
又BG＝BH ∴∠3＝∠4
∴∠BGA＝∠BHC ………………………………………………（5＇）
∴△BGA≌△BHC（ASA） ……………………………………（6＇）
∴AB＝BC ……………………………………………………（7＇）
∴□ABCD為菱形……………………………………………（8＇）
閱讀快車系列答案科目：初中數學 來源： 題型：
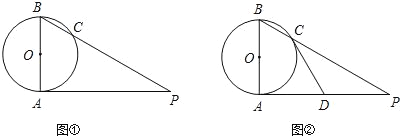
【題目】已知AB是⊙O的直徑，AP是⊙O的切線，A是切點，BP與⊙O交于點C．
（1）如圖①，若∠P=35°，求∠ABP的度數；
（2）如圖②，若D為AP的中點，求證：直線CD是⊙O的切線．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知E，F分別為正方形ABCD的邊AB，BC的中點，AF與DE交于點M，O為BD的中點，則下列結論：①∠AME=90°；②∠BAF=∠EDB；③∠BMO=90°；④MD=2AM=4EM；⑤
．其中正確結論的是（ ）
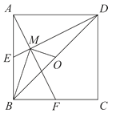
A. ①③④B. ②④⑤C. ①③⑤D. ①③④⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
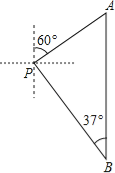
【題目】小亮一家在一湖泊中游玩，湖泊中有一孤島，媽媽在孤島P處觀看小亮與爸爸在湖中劃船（如圖所示）．小船從P處出發，沿北偏東60°方向劃行200米到A處，接著向正南方向劃行一段時間到B處．在B處小亮觀測到媽媽所在的P處在北偏西37°的方向上，這時小亮與媽媽相距多少米（精確到1米）？
（參考數據：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，
≈1.41，
≈1.73）
查看答案和解析>>
科目：初中數學 來源： 題型：
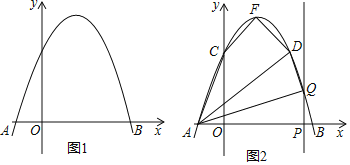
【題目】如圖1，拋物線y=ax2+bx+3交x軸于點A（﹣1，0）和點B（3，0）．
（1）求該拋物線所對應的函數解析式；
（2）如圖2，該拋物線與y軸交于點C，頂點為F，點D（2，3）在該拋物線上．
①求四邊形ACFD的面積；
②點P是線段AB上的動點（點P不與點A、B重合），過點P作PQ⊥x軸交該拋物線于點Q，連接AQ、DQ，當△AQD是直角三角形時，求出所有滿足條件的點Q的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
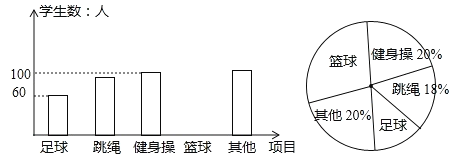
【題目】某市為提高學生參與體育活動的積極性，圍繞“你喜歡的體育運動項目（只寫一項）”這一問題，對初一新生進行隨機抽樣調查．下面是根據調查結果繪制成的統計圖（不完整）．
請你根據圖中提供的信息解答下列問題：
（1）本次抽樣調查一共調查調查了多少名學生？
（2）根據條形統計圖中的數據，求扇形統計圖中“最喜歡足球運動”的學生數對應扇形的圓心角度數．
（3）請將條形圖補充完整．
（4）若該市2017年約有初一新生21000人，請你估計全市本屆學生中“最喜歡足球運動”的學生有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有七張正面分別標有數字﹣1、﹣2、0、1、2、3、4的卡片，除數字不同外其余全部相同，現將它們背面朝上，洗勻后從中隨機抽取一張，記卡片上的數字為m，則使關于x的方程x2﹣2（m﹣1）x+m2﹣3m＝0有實數根，且不等式組
無解的概率是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，A（4，3）是反比例函數y=
在第一象限圖象上一點，連接OA，過A作AB∥x軸，截取AB=OA（B在A右側），連接OB，交反比例函數y=的圖象于點P．
（1）求反比例函數y=的表達式；
（2）求點B的坐標；
（3）求△OAP的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某日的錢塘江觀潮信息如表：
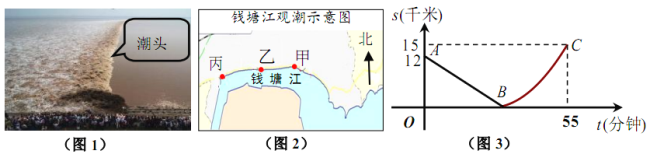
按上述信息，小紅將“交叉潮”形成后潮頭與乙地之間的距離
（千米）與時間
（分鐘）的函數關系用圖3表示，其中：“11:40時甲地‘交叉潮’的潮頭離乙地12千米”記為點
，點
坐標為
，曲線
可用二次函數
（
，
是常數）刻畫．
（1）求
的值，并求出潮頭從甲地到乙地的速度；
（2）11:59時，小紅騎單車從乙地出發，沿江邊公路以
千米/分的速度往甲地方向去看潮，問她幾分鐘后與潮頭相遇？
（3）相遇后，小紅立即調轉車頭，沿江邊公路按潮頭速度與潮頭并行，但潮頭過乙地后均勻加速，而單車最高速度為
千米/分，小紅逐漸落后，問小紅與潮頭相遇到落后潮頭1.8千米共需多長時間？（潮水加速階段速度
，
是加速前的速度）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com