分析:(1)令y=0,即y=
x
2-
(b+1)x+
=0,解關(guān)于x的一元二次方程即可求出A,B橫坐標(biāo),令x=0,求出y的值即C的縱坐標(biāo);
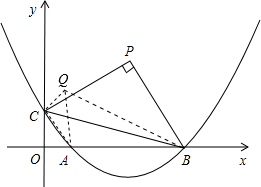
(2)存在,先假設(shè)存在這樣的點(diǎn)P,使得四邊形PCOB的面積等于2b,且△PBC是以點(diǎn)P為直角頂點(diǎn)的等腰直角三角形.設(shè)點(diǎn)P的坐標(biāo)為(x,y),連接OP,過P作PD⊥x軸,PE⊥y軸,垂足分別為D、E,利用已知條件證明△PEC≌△PDB,進(jìn)而求出x和y的值,從而求出P的坐標(biāo);
(3)存在,假設(shè)存在這樣的點(diǎn)Q,使得△QCO,△QOA和△QAB中的任意兩個(gè)三角形均相似,有條件可知:要使△QOA與△QAB相似,只能∠QAO=∠BAQ=90°,即QA⊥x軸;要使△QOA與△OQC相似,只能∠QCO=90°或∠OQC=90°;再分別討論求出滿足題意Q的坐標(biāo)即可.
解答:解:(1)令y=0,即y=
x
2-
(b+1)x+
=0,
解得:x=1或b,
∵b是實(shí)數(shù)且b>2,點(diǎn)A位于點(diǎn)B的左側(cè),
∴點(diǎn)B的坐標(biāo)為(b,0),
令x=0,
解得:y=
,
∴點(diǎn)C的坐標(biāo)為(0,
),
故答案為:(b,0),(0,
);
(2)存在,
假設(shè)存在這樣的點(diǎn)P,使得四邊形PCOB的面積等于2b,且△PBC是以點(diǎn)P為直角頂點(diǎn)的等腰直角三角形.
設(shè)點(diǎn)P的坐標(biāo)為(x,y),連接OP.
則S
四邊形PCOB=S
△PCO+S
△POB=
•
•x+
•b•y=2b,
∴x+4y=16.
過P作PD⊥x軸,PE⊥y軸,垂足分別為D、E,
∴∠PEO=∠EOD=∠ODP=90°.
∴四邊形PEOD是矩形.

∴∠EPD=90°.
∴∠EPC=∠DPB.
∴△PEC≌△PDB,∴PE=PD,即x=y.
由
解得
由△PEC≌△PDB得EC=DB,即
-
=b-
,
解得b=
>2符合題意.
∴P的坐標(biāo)為(
,
);
(3)假設(shè)存在這樣的點(diǎn)Q,使得△QCO,△QOA和△QAB中的任意兩個(gè)三角形均相似.
∵∠QAB=∠AOQ+∠AQO,
∴∠QAB>∠AOQ,∠QAB>∠AQO.
∴要使△QOA與△QAB相似,只能∠QAO=∠BAQ=90°,即QA⊥x軸.
∵b>2,
∴AB>OA,
∴∠Q0A>∠ABQ.
∴只能∠AOQ=∠AQB.此時(shí)∠OQB=90°,
由QA⊥x軸知QA∥y軸.
∴∠COQ=∠OQA.
∴要使△QOA與△OQC相似,只能∠QCO=90°或∠OQC=90°.
(I)當(dāng)∠OCQ=90°時(shí),△CQO≌△QOA.
∴AQ=CO=
.
由AQ
2=OA•AB得:(
)
2=b-1.
解得:b=8±4
.
∵b>2,
∴b=8+4
.
∴點(diǎn)Q的坐標(biāo)是(1,2+
).
(II)當(dāng)∠OQC=90°時(shí),△OCQ∽△QOA,
∴
=
,即OQ
2=OC•AQ.
又OQ
2=OA•OB,
∴OC•AQ=OA•OB.即
•AQ=1×b.
解得:AQ=4,此時(shí)b=17>2符合題意,
∴點(diǎn)Q的坐標(biāo)是(1,4).
∴綜上可知,存在點(diǎn)Q(1,2+
)或Q(1,4),使得△QCO,△QOA和△QAB中的任意兩個(gè)三角形均相似.

 角形均相似(全等可作相似的特殊情況)?如果存在,求出點(diǎn)Q的坐標(biāo);如果不存在,請(qǐng)說明理由.
角形均相似(全等可作相似的特殊情況)?如果存在,求出點(diǎn)Q的坐標(biāo);如果不存在,請(qǐng)說明理由.




 (2012•蘇州)如圖,矩形ABCD的對(duì)角線AC、BD相交于點(diǎn)O,CE∥BD,DE∥AC,若AC=4,則四邊形CODE的周長(zhǎng)( )
(2012•蘇州)如圖,矩形ABCD的對(duì)角線AC、BD相交于點(diǎn)O,CE∥BD,DE∥AC,若AC=4,則四邊形CODE的周長(zhǎng)( ) (cm),其中0≤x≤2.5.
(cm),其中0≤x≤2.5.
 (2012•蘇州)如圖,已知BD是⊙O的直徑,點(diǎn)A、C在⊙O上,
(2012•蘇州)如圖,已知BD是⊙O的直徑,點(diǎn)A、C在⊙O上,
