
【題目】在平面直角坐標(biāo)系中,將二次函數(shù)![]() 的圖象向右平移1個單位,再向下平移2個單位,得到如圖所示的拋物線,該拋物線與
的圖象向右平移1個單位,再向下平移2個單位,得到如圖所示的拋物線,該拋物線與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 、
、![]() (點(diǎn)
(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的左側(cè)),
的左側(cè)),![]() ,經(jīng)過點(diǎn)
,經(jīng)過點(diǎn)![]() 的一次函數(shù)
的一次函數(shù)![]() 的圖象與
的圖象與![]() 軸正半軸交于點(diǎn)
軸正半軸交于點(diǎn)![]() ,且與拋物線的另一個交點(diǎn)為
,且與拋物線的另一個交點(diǎn)為![]() ,
,![]() 的面積為5.
的面積為5.
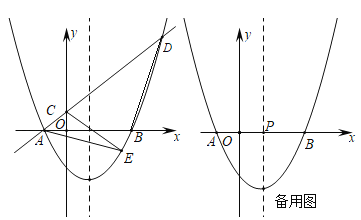
(1)求拋物線和一次函數(shù)的解析式;
(2)拋物線上的動點(diǎn)![]() 在一次函數(shù)的圖象下方,求
在一次函數(shù)的圖象下方,求![]() 面積的最大值,并求出此時點(diǎn)E的坐標(biāo);
面積的最大值,并求出此時點(diǎn)E的坐標(biāo);
(3)若點(diǎn)![]() 為
為![]() 軸上任意一點(diǎn),在(2)的結(jié)論下,求
軸上任意一點(diǎn),在(2)的結(jié)論下,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() 的面積最大值是
的面積最大值是![]() ,此時
,此時![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() ;(3)
;(3)![]() 的最小值是3.
的最小值是3.
【解析】
(1)先寫出平移后的拋物線解析式,再把點(diǎn)![]() 代入可求得
代入可求得![]() 的值,由
的值,由![]() 的面積為5可求出點(diǎn)
的面積為5可求出點(diǎn)![]() 的縱坐標(biāo),代入拋物線解析式可求出橫坐標(biāo),由
的縱坐標(biāo),代入拋物線解析式可求出橫坐標(biāo),由![]() 、
、![]() 的坐標(biāo)可利用待定系數(shù)法求出一次函數(shù)解析式;
的坐標(biāo)可利用待定系數(shù)法求出一次函數(shù)解析式;
(2)作![]() 軸交
軸交![]() 于
于![]() ,如圖,利用三角形面積公式,由
,如圖,利用三角形面積公式,由![]() 構(gòu)建關(guān)于E點(diǎn)橫坐標(biāo)的二次函數(shù),然后利用二次函數(shù)的性質(zhì)即可解決問題;
構(gòu)建關(guān)于E點(diǎn)橫坐標(biāo)的二次函數(shù),然后利用二次函數(shù)的性質(zhì)即可解決問題;
(3)作![]() 關(guān)于
關(guān)于![]() 軸的對稱點(diǎn)
軸的對稱點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,則
,則![]() ,利用銳角三角函數(shù)的定義可得出
,利用銳角三角函數(shù)的定義可得出![]() ,此時
,此時![]() 最小,求出最小值即可.
最小,求出最小值即可.
解:(1)將二次函數(shù)![]() 的圖象向右平移1個單位,再向下平移2個單位,得到的拋物線解析式為
的圖象向右平移1個單位,再向下平移2個單位,得到的拋物線解析式為![]() ,
,
∵![]() ,∴點(diǎn)
,∴點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
代入拋物線的解析式得,![]() ,∴
,∴![]() ,
,
∴拋物線的解析式為![]() ,即
,即![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() 的面積為5,∴
的面積為5,∴![]() ,∴
,∴![]() ,
,
代入拋物線解析式得,![]() ,解得
,解得![]() ,
,![]() ,∴
,∴![]() ,
,
設(shè)直線![]() 的解析式為
的解析式為![]() ,
,
∴ ,解得:
,解得:![]() ,
,
∴直線![]() 的解析式為
的解析式為![]() .
.
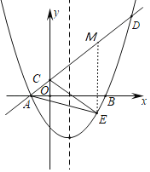
(2)過點(diǎn)![]() 作
作![]() 軸交
軸交![]() 于
于![]() ,如圖,設(shè)
,如圖,設(shè)![]() ,則
,則![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,![]() ,
,
∴當(dāng)![]() 時,
時,![]() 的面積有最大值,最大值是
的面積有最大值,最大值是![]() ,此時
,此時![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() .
.
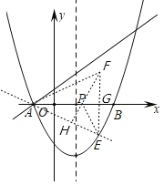
(3)作![]() 關(guān)于
關(guān)于![]() 軸的對稱點(diǎn)
軸的對稱點(diǎn)![]() ,連接
,連接![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴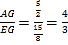 ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 、
、![]() 關(guān)于
關(guān)于![]() 軸對稱,∴
軸對稱,∴![]() ,
,
∴![]() ,此時
,此時![]() 最小,
最小,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() 的最小值是3.
的最小值是3.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
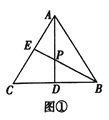
【題目】[問題發(fā)現(xiàn)]
如圖①,在![]() 中,點(diǎn)
中,點(diǎn)![]() 是
是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在邊
在邊![]() 上,
上,![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,若
,若![]() ,則
,則![]() _____ ;
_____ ;
[拓展提高]
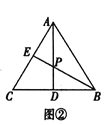
如圖②,在等邊三角形![]() 中,點(diǎn)
中,點(diǎn)![]() 是
是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在邊
在邊![]() 上,直線
上,直線![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
[解決問題]
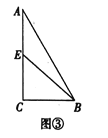
如圖③,在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在直線
在直線![]() 上,直線
上,直線![]() 與直線
與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,![]() .請直接寫出
.請直接寫出![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
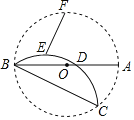
【題目】如圖,AB是⊙O的直徑,BC是弦,沿BC對折劣弧BC,交AB于D,點(diǎn)E、F分別是弧AB和弧BD的中點(diǎn).若AD=4,AB=10,則EF=_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
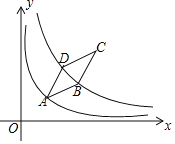
【題目】如圖,菱形ABCD頂點(diǎn)A在函數(shù)y=![]() (x>0)的圖像上,函數(shù)y=
(x>0)的圖像上,函數(shù)y=![]() (k>4,x>0)的圖象關(guān)于直線AC對稱,且經(jīng)過點(diǎn)B、D兩點(diǎn),若AB=4,∠ADC=150°,則k=______。
(k>4,x>0)的圖象關(guān)于直線AC對稱,且經(jīng)過點(diǎn)B、D兩點(diǎn),若AB=4,∠ADC=150°,則k=______。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】同時擲兩個質(zhì)地均勻的骰子,觀察向上一面的點(diǎn)數(shù),兩個骰子的點(diǎn)數(shù)相同的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
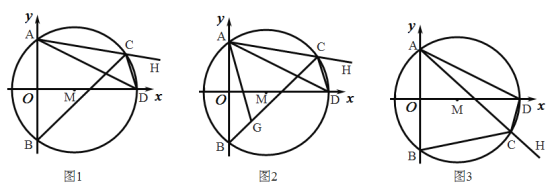
【題目】如圖1,在平面直角坐標(biāo)系中,已知![]() 的半徑為5,圓心
的半徑為5,圓心![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,交
,交![]() 軸于
軸于![]() ,
,![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 是
是![]() 上的一點(diǎn)(不與點(diǎn)
上的一點(diǎn)(不與點(diǎn)![]() 、
、![]() 、
、![]() 重合),連結(jié)
重合),連結(jié)![]() 并延長,連結(jié)
并延長,連結(jié)![]() ,
,![]() ,
,![]() .
.
(1)求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)當(dāng)點(diǎn)![]() 在
在![]() 上時.
上時.
①求證:![]() ;
;
②如圖2,在![]() 上取一點(diǎn)
上取一點(diǎn)![]() ,使
,使![]() ,連結(jié)
,連結(jié)![]() .求證:
.求證:![]() ;
;
(3)如圖3,當(dāng)點(diǎn)![]() 在
在![]() 上運(yùn)動的過程中,試探究
上運(yùn)動的過程中,試探究![]() 的值是否發(fā)生變化?若不變,請直接寫出該定值;若變化,請說明理由.
的值是否發(fā)生變化?若不變,請直接寫出該定值;若變化,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)y=x2+2kx+k﹣1(k為常數(shù)),下列說法正確的個數(shù)是( )
(1)對任意實(shí)數(shù)k,函數(shù)與x軸有兩個交點(diǎn)
(2)當(dāng)x≥﹣k時,函數(shù)y的值都隨x的增大而增大
(3)k取不同的值時,二次函數(shù)y的頂點(diǎn)始終在同一條拋物線上
(4)對任意實(shí)數(shù)k,拋物線y=x2+2kx+k﹣1都必定經(jīng)過唯一定點(diǎn)
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】黃山景區(qū)銷售一種旅游紀(jì)念品,已知每件進(jìn)價為![]() 元,當(dāng)銷售單價定為
元,當(dāng)銷售單價定為![]() 元時,每天可以銷售
元時,每天可以銷售![]() 件.市場調(diào)查反映:銷售單價每提高
件.市場調(diào)查反映:銷售單價每提高![]() 元,日銷量將會減少
元,日銷量將會減少![]() 件.物價部門規(guī)定:銷售單價不低于
件.物價部門規(guī)定:銷售單價不低于![]() 元,但不能超過
元,但不能超過![]() 元,設(shè)該紀(jì)念品的銷售單價為
元,設(shè)該紀(jì)念品的銷售單價為![]() (元),日銷量為
(元),日銷量為![]() (件).
(件).
(1)直接寫出![]() 與
與![]() 的函數(shù)關(guān)系式.
的函數(shù)關(guān)系式.
(2)求日銷售利潤![]() (元)與銷售單價
(元)與銷售單價![]() (元)的函數(shù)關(guān)系式.并求當(dāng)
(元)的函數(shù)關(guān)系式.并求當(dāng)![]() 為何值時,日銷售利潤最大,最大利潤是多少?
為何值時,日銷售利潤最大,最大利潤是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,數(shù)學(xué)興趣小組的小穎想測量教學(xué)樓前的一棵樹的樹高,下午課外活動時她測得一根長為1m的竹竿的影長是0.8m,但當(dāng)她馬上測量樹高時,發(fā)現(xiàn)樹的影子不全落在地面上,有一部分影子落在教學(xué)樓的墻壁上(如圖),他先測得留在墻壁上的影高為1.2m,又測得地面的影長為2.6m,請你幫她算一下,樹高是( )
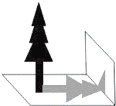
A.4.25mB.4.45mC.4.60mD.4.75m
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com