
【題目】如圖,拋物線y=ax2+bx+2與x軸交于點(diǎn)A(﹣1,0)和點(diǎn)B(2,0),與y軸交于點(diǎn)C.
(1)求該拋物線的函數(shù)解析式;
(2)如圖1,連接BC,點(diǎn)D是BC上方拋物線上的動(dòng)點(diǎn),連接OD、CD,OD交BC于點(diǎn)F,當(dāng)![]() 時(shí),求
時(shí),求![]() 的值;
的值;
(3)如圖2,點(diǎn)E的坐標(biāo)為![]() ,在拋物線上是否存在點(diǎn)P,使∠OBP=2∠OBE?若存在,請(qǐng)求出符合條件的點(diǎn)P的橫坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
,在拋物線上是否存在點(diǎn)P,使∠OBP=2∠OBE?若存在,請(qǐng)求出符合條件的點(diǎn)P的橫坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,x=
;(3)存在,x=![]() 或 x=
或 x=![]()
【解析】
(1)把點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 代入
代入![]() 即可求得拋物線解析式;
即可求得拋物線解析式;
(2)過(guò)點(diǎn)![]() 作
作![]() 軸交
軸交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,根據(jù)
,根據(jù)![]() ,得出
,得出![]() ,證明
,證明![]() ,得出
,得出![]() ,設(shè)
,設(shè)![]() ,則
,則![]() ,得出
,得出![]() ,解出
,解出![]() 即可得
即可得![]() ,
,![]() ,根據(jù)
,根據(jù)![]() 可得出答案;
可得出答案;
(3)分點(diǎn)![]() 在
在![]() 軸上方、點(diǎn)
軸上方、點(diǎn)![]() 在
在![]() 軸下方兩種情況,分別求解即可.
軸下方兩種情況,分別求解即可.
解:(1)![]() ,
,![]() ,
,
![]() 把
把![]() ,
,![]() 代入
代入![]() 得,
得,
![]() ,
,
解得,![]() ,
,
![]() 該拋物線的函數(shù)解析式為
該拋物線的函數(shù)解析式為![]() ;
;
(2)如圖1,過(guò)點(diǎn)![]() 作
作![]() 軸交
軸交![]() 于點(diǎn)
于點(diǎn)![]() ,交.
,交.![]() .軸于點(diǎn)
.軸于點(diǎn)![]() ,
,
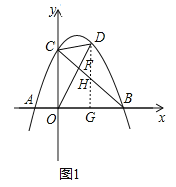
![]() 拋物線
拋物線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,
,
![]() ,
,
設(shè)直線![]() 解析式為
解析式為![]() ,
,
則![]() ,解得
,解得![]() ,
,
![]() 直線
直線![]() 解析式為
解析式為![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]()
![]() .
.
(3)①當(dāng)點(diǎn)![]() 在
在![]() 軸上方時(shí),
軸上方時(shí),
在![]() 軸上取點(diǎn)
軸上取點(diǎn)![]() ,連接
,連接![]() ,則
,則![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作直線
作直線![]() 交拋物線于點(diǎn)
交拋物線于點(diǎn)![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,使
,使![]() ,
,
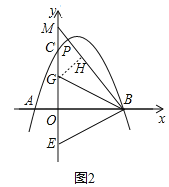
則![]() ,
,
過(guò)點(diǎn)![]() 作
作![]() ,
,
![]() ,
,
![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
解得:![]() ,
,
故![]() ,
,
![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() ,
,
將點(diǎn)![]() 、
、![]() 的坐標(biāo)代入一次函數(shù)表達(dá)式
的坐標(biāo)代入一次函數(shù)表達(dá)式![]() ,
,
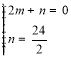 ,
,
解得: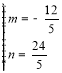 ,
,
![]() 直線
直線![]() 的表達(dá)式為:
的表達(dá)式為:![]() ,
,
![]()
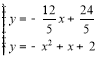 ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
②當(dāng)點(diǎn)![]() 在
在![]() 軸下方時(shí),
軸下方時(shí),
作點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸的對(duì)稱點(diǎn)
軸的對(duì)稱點(diǎn)![]() ,
,
求得直線![]() 的解析式為
的解析式為![]() ,
,
![]()
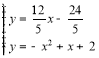 ,
,
解得,![]() 或
或![]() (舍去),
(舍去),
綜合以上可得,點(diǎn)![]() 的橫坐標(biāo)是
的橫坐標(biāo)是![]() 或
或 ![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】若![]() ,則二次函數(shù)
,則二次函數(shù)![]() 的圖象的頂點(diǎn)在 ( )
的圖象的頂點(diǎn)在 ( )
A.第一象限;B.第二象限;C.第三象限;D.第四象限
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是由邊長(zhǎng)為1的小正方形構(gòu)成的網(wǎng)格,每個(gè)小正方形的頂點(diǎn)叫格點(diǎn),![]() 的頂點(diǎn)都在格點(diǎn)上,僅用無(wú)刻度的直尺在網(wǎng)格中畫(huà)圖(保留作圖連線痕跡),并回答問(wèn)題.
的頂點(diǎn)都在格點(diǎn)上,僅用無(wú)刻度的直尺在網(wǎng)格中畫(huà)圖(保留作圖連線痕跡),并回答問(wèn)題.
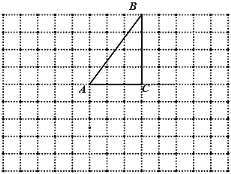
(1)在![]() 的右邊找格點(diǎn)
的右邊找格點(diǎn)![]() ,連
,連![]() ,使
,使![]() 平分
平分![]() .
.
(2)若![]() 與
與![]() 交于
交于![]() ,直接寫出
,直接寫出![]() 的值.
的值.
(3)找格點(diǎn)![]() ,連
,連![]() ,使
,使![]() 于
于![]() .
.
(4)在![]() 上找點(diǎn)
上找點(diǎn)![]() ,連
,連![]() ,使
,使![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為推進(jìn)“傳統(tǒng)文化進(jìn)校園”活動(dòng),我市某中學(xué)舉行了“走進(jìn)經(jīng)典”征文比賽,賽后整理參賽學(xué)生的成績(jī),將學(xué)生的成績(jī)分為![]() 四個(gè)等級(jí),并將結(jié)果繪制成不完整的條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖.請(qǐng)根據(jù)統(tǒng)計(jì)圖解答下列問(wèn)題:
四個(gè)等級(jí),并將結(jié)果繪制成不完整的條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖.請(qǐng)根據(jù)統(tǒng)計(jì)圖解答下列問(wèn)題:
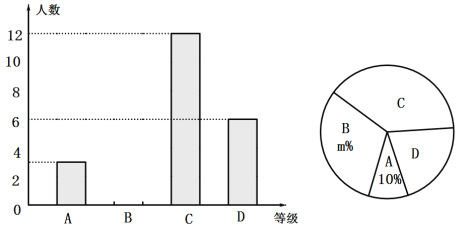
(1)參加征文比賽的學(xué)生共有 人;
(2)補(bǔ)全條形統(tǒng)計(jì)圖;
(3)在扇形統(tǒng)計(jì)圖中,表示![]() 等級(jí)的扇形的圓心角為__ 圖中
等級(jí)的扇形的圓心角為__ 圖中![]() ;
;
(4)學(xué)校決定從本次比賽獲得![]() 等級(jí)的學(xué)生中選出兩名去參加市征文比賽,已知
等級(jí)的學(xué)生中選出兩名去參加市征文比賽,已知![]() 等級(jí)中有男生一名,女生兩名,請(qǐng)用列表或畫(huà)樹(shù)狀圖的方法求出所選兩名學(xué)生恰好是一名男生和一名女生的概率.
等級(jí)中有男生一名,女生兩名,請(qǐng)用列表或畫(huà)樹(shù)狀圖的方法求出所選兩名學(xué)生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列命題中
①三角形的外心到三角形的三個(gè)頂點(diǎn)的距離相等
②兩條對(duì)角線相等的四邊形是矩形
③將一次函數(shù)y=3x﹣1的圖象不經(jīng)過(guò)第四象限
④點(diǎn)A(x1,y1),B(x2,y2)都在反比例函數(shù)y=![]() 圖象上,且x1<x2,則y1<y2
圖象上,且x1<x2,則y1<y2
其中真命題有( )個(gè)
A.4個(gè)B.3個(gè)C.2個(gè)D.1個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某班為了解學(xué)生一學(xué)期做義工的時(shí)間情況,對(duì)全班50名學(xué)生進(jìn)行調(diào)查,按做義工的時(shí)間![]() (單位:小時(shí)),將學(xué)生分成五類:
(單位:小時(shí)),將學(xué)生分成五類: ![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),繪制成尚不完整的條形統(tǒng)計(jì)圖如圖11.
),繪制成尚不完整的條形統(tǒng)計(jì)圖如圖11.
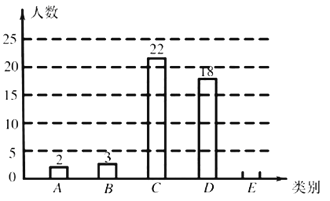
根據(jù)以上信息,解答下列問(wèn)題:
(1)![]() 類學(xué)生有 人,補(bǔ)全條形統(tǒng)計(jì)圖;
類學(xué)生有 人,補(bǔ)全條形統(tǒng)計(jì)圖;
(2)![]() 類學(xué)生人數(shù)占被調(diào)查總?cè)藬?shù)的 %;
類學(xué)生人數(shù)占被調(diào)查總?cè)藬?shù)的 %;
(3)從該班做義工時(shí)間在![]() 的學(xué)生中任選2人,求這2人做義工時(shí)間都在
的學(xué)生中任選2人,求這2人做義工時(shí)間都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,一次函數(shù)![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù)![]() 的圖象交于點(diǎn)
的圖象交于點(diǎn)![]() ,與
,與![]() 交于點(diǎn)
交于點(diǎn)![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,且
,且![]() .
.
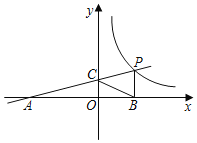
(1)求一次函數(shù)和反比例函數(shù)的解析式;
(2)點(diǎn)![]() 為反比例函數(shù)圖象上使得四邊形
為反比例函數(shù)圖象上使得四邊形![]() 為菱形的一點(diǎn),點(diǎn)
為菱形的一點(diǎn),點(diǎn)![]() 為
為![]() 軸上的一動(dòng)點(diǎn),當(dāng)
軸上的一動(dòng)點(diǎn),當(dāng)![]() 最大時(shí),求點(diǎn)
最大時(shí),求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為進(jìn)一步提升學(xué)生的法律素質(zhì),中學(xué)組織學(xué)生開(kāi)展《憲法》知識(shí)競(jìng)賽,該學(xué)校隨機(jī)抽取部分學(xué)生的成績(jī)并進(jìn)行統(tǒng)計(jì)分析,以了解學(xué)生的法律知識(shí)水平.根據(jù)這些學(xué)生的競(jìng)賽成績(jī)分布情況,將競(jìng)賽成績(jī)分為甲、乙、丙、丁、戊五個(gè)等級(jí).圖表如下:
等級(jí) | 分?jǐn)?shù)/分 | 頻數(shù) | 各組總分/分 |
甲 |
| 39 | 2184 |
乙 |
| 75 | 5175 |
丙 |
| 120 | 9720 |
丁 |
|
| 4050 |
戊 |
| 21 | 2037 |

(1)求![]() 的值;
的值;
(2)競(jìng)賽成績(jī)的中位數(shù)落在哪個(gè)等級(jí)?
(3)求這組競(jìng)賽成績(jī)的平均值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() ,拋物線
,拋物線![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
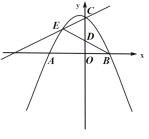

備用圖
(1)求拋物線的解析式.
(2)點(diǎn)![]() 是直線
是直線![]() 上方的拋物線上一點(diǎn),連接
上方的拋物線上一點(diǎn),連接![]() 、
、![]() 、
、![]() ,
,![]() 與
與![]() 軸交于
軸交于![]() .
.
①點(diǎn)![]() 是
是![]() 軸上一動(dòng)點(diǎn),連接
軸上一動(dòng)點(diǎn),連接![]() ,當(dāng)以
,當(dāng)以![]() 、
、![]() 、
、![]() 為頂點(diǎn)的三角形與
為頂點(diǎn)的三角形與![]() 相似時(shí),求出線段
相似時(shí),求出線段![]() 的長(zhǎng);
的長(zhǎng);
②點(diǎn)![]() 為
為![]() 軸左側(cè)拋物線上一點(diǎn),過(guò)點(diǎn)
軸左側(cè)拋物線上一點(diǎn),過(guò)點(diǎn)![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,若
,若![]() ,請(qǐng)直接寫出點(diǎn)
,請(qǐng)直接寫出點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com