
【題目】如圖,點E為正方形ABCD的邊BC所在直線上的一點,連接AE,過點C作CF⊥AE于F,連接BF.

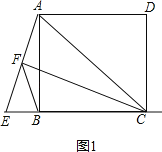
(1)如圖1,當點E在CB的延長線上,且AC=EC時,求證:BF=![]() ;
;
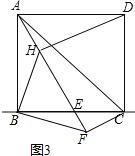
(2)如圖2,當點E在線段BC上,且AE平分∠BAC時,求證:AB+BE=AC;
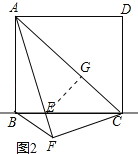
(3)如圖3,當點E繼續往右運動到BC中點時,過點D作DH⊥AE于H,連接BH.求證:∠BHF=45°.
【答案】見解析
【解析】
試題分析:(1)根據等腰三角形的性質和直角三角形斜邊中線的性質即可證得結論;
(2)作EG⊥AC于G,根據角平分線的性質得出BE=EG,進而通過RT△ABE≌RT△AGE得出AG=AB,然后證得△EGC是等腰直角三角形,從而證得EG=GC,即可證得AB+BE=AC;
(3)設正方形的邊長為1,則AB=AD=1,BE=EC=![]() ,根據勾股定理求得AE=
,根據勾股定理求得AE=![]() ,然后通過證得△AEB∽△CEF,△ADH∽△EAB,對應邊成比例證得CF=AH=
,然后通過證得△AEB∽△CEF,△ADH∽△EAB,對應邊成比例證得CF=AH=![]() ,然后根據SAS證得△ABH≌△CBF,證得BH=BF,∠ABH=∠CBF,從而證得△HBF是等腰直角三角形,從而證得∠BHF=45°.
,然后根據SAS證得△ABH≌△CBF,證得BH=BF,∠ABH=∠CBF,從而證得△HBF是等腰直角三角形,從而證得∠BHF=45°.
(1)證明:如圖1,∵AC=EC,CF⊥AE,
∴AF=EF,
∴BF是RT△ABE的斜邊的中線,
∴BF=![]() AE;
AE;
(2)如圖2,作EG⊥AC于G,
∵AE平分∠BAC,AB⊥BE,
∴BE=EG,
在RT△ABE和RT△AGE中
![]() ,
,
∴RT△ABE≌RT△AGE(HL),
∴AG=AB,
∵四邊形ABCD是正方形,
∴∠ACB=45°,
∴∠GEC=45°,
∴∠GEC=∠ACB=45°,
∴EG=GC,
∴AB+BE=AG+GC,
即AB+BE=AC;
(3)如圖3,設正方形的邊長為1,則AB=AD=1,
∵點E是BC中點,
∴BE=EC=![]() ,
,
∴AE=![]() =
=![]() ,
,
∵∠ABE=∠CFE=90°,∠AEB=∠CEF,
∴△AEB∽△CEF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CF=![]() ,
,
∵AD∥BC,
∴∠DAH=∠AEB,
∵∠AHD=∠BEA=90°,
∴△ADH∽△EAB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AH=![]() ,
,
∴CF=AH,
在△ABH和△CBF中
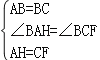
∴△ABH≌△CBF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠ABH+∠HBE=∠ABE=90°,
∴∠HBF=90°,
∴△HBF是等腰直角三角形,
∴∠BHF=45°.


科目:初中數學 來源: 題型:
【題目】計算:
(1)|-1|+(—2)3+(7-π)0-(![]() )-1;
)-1;
(2) (-2a)3·(a2)2÷a3
(3) (3a+b-2)(3a-b+2)
(4)10002-1002×998
(5) (x+1)(x2+1)(x4+1)(x-1)
(6) (3a+2)2(3a-2)2
查看答案和解析>>
科目:初中數學 來源: 題型:
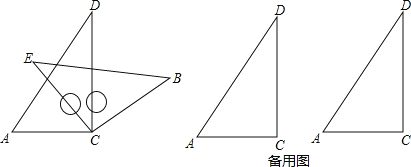
【題目】將一副三角板中的兩塊直角三角尺的直角頂點C按如圖方式疊放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,則∠ACB的度數為 ;
②若∠ACB=140°,求∠DCE的度數;
(2)由(1)猜想∠ACB與∠DCE的數量關系,并說明理由.
(3)當∠ACE<180°且點E在直線AC的上方時,這兩塊三角尺是否存在一組邊互相平行?若存在,請直接寫出∠ACE角度所有可能的值(不必說明理由);若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個二元碼是由0和1組成的數字串x1x2…xn(n為正整數),其中xk(k=1,2,…,n)稱為第k位碼元,如:二元碼01101的第1位碼元為0,第5位碼元為1。
(1)二元碼100100的第4位碼元為__________;
(2)二元碼是通信中常用的碼,但在通信過程中有時會發生碼元錯誤(即碼元由0變為1,或者由1變為0)。已知某種二元碼x1x2…x7的碼元滿足如下校驗方程組:

其中運算![]() 定義為:0
定義為:0![]() 0=0,1
0=0,1![]() 1=0,0
1=0,0![]() 1=1,1
1=1,1![]() 0=1。
0=1。
①計算:0![]() 1
1![]() 1
1![]() 0=___________;
0=___________;
②現已知一個這種二元碼在通信過程中僅在第k位發生碼元錯誤后變成了0101101,那么利用上述校驗方程組可判定k等于__________。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀,然后解答提出的問題:
設a,b是有理數,且滿足a+![]() b=3﹣2
b=3﹣2![]() ,求ba的值.
,求ba的值.
解:由題意得(a﹣3)+(b+2)![]() =0,因為a,b都是有理數,所以a﹣3,b+2也是有理數,
=0,因為a,b都是有理數,所以a﹣3,b+2也是有理數,
由于![]() 是無理數,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.問題:設x,y都是有理數,且滿足x2﹣2y+
是無理數,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.問題:設x,y都是有理數,且滿足x2﹣2y+![]() y=8+4
y=8+4![]() ,求x+y的值.
,求x+y的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C在射線OA上,CE平分∠ACD. OF平分∠COB并與射線CD交于點F。
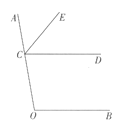
(1)依題意補全圖形;
(2)若∠COB+∠OCD=180°,求證:∠ACE=∠COF。
請將下面的證明過程補充完整。
證明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE=______________,∠COF=![]() ∠COB。
∠COB。
(理由: _____________________________________)
∵點C在射線OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠____________。
(理由: ___________________________________)
∴∠ACE=∠COF。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班七個興趣小組人數分別為4,4,5,x,6,6,7.已知這組數據的平均數是5,則這組數據的中位數是( )
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com