已知⊙O的半徑是5cm,弦AB∥CD,AB=6cm,CD=8cm,則AB與CD的距離是 .
【答案】
分析:本題有兩種情況,即AB,CD在圓心O的同側或兩側兩種情況,需分類討論.
解答: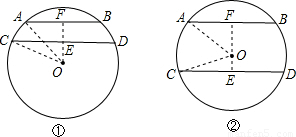
解:(1)如圖①,過O作OF⊥AB于F交CD于E,連接OA,OC,
∵AB∥CD,
∴OE⊥CD;
由垂徑定理得AF=FB=

AB=3,CE=DE=

CD=4,
∴OF=
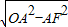
=4,OE=
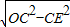
=3,
∴EF=OF-OE=1cm;
(2)過O作OF⊥AB于F,OE⊥CD于E,連接AO,CO,
同理可得OF=4cm,OE=3cm,
當AB,CD在圓心O的兩側時,
EF=OF+OE=7(cm),
∴AB與CD的距離為7cm或1cm.
點評:此題主要考查的是勾股定理及垂徑定理的應用,需注意AB、CD的位置關系有兩種,不要漏解.

 閱讀快車系列答案
閱讀快車系列答案