
【題目】如圖,O為直線AB上一點,∠AOC=50°,OD平分∠AOC,∠DOE=90度.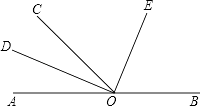
(1)請你數一數,圖中有多少個角;
(2)求出∠BOD的度數;
(3)請通過計算說明OE是否平分∠BOC.
【答案】
(1)解:圖中有9個小于平角的角
(2)解:因為OD平分∠AOC,∠AOC=50°
所以∠AOD= ![]() =25°,所以∠BOD=180°﹣25°=155°
=25°,所以∠BOD=180°﹣25°=155°
(3)解:因為∠BOE=180°﹣∠DOE﹣∠AOD=180°﹣90°﹣25°=65°
∠COE=90°﹣25°=65°
所以∠BOE=∠COE.即OE平分∠BOC
【解析】(1)按照順序數,以OA為邊順時針數有3個角,以OD為邊的有3個角,以OC為邊的有2個角,以OE為邊的有1個角,一共由9個角。
(2)觀察圖形及已知條件∠BOD=180°-∠AOD,只需求出∠AOD的度數,根據角平分線的定義易求出。
(3)根據題意分別求出∠BOE和∠COE的度數即可判斷。


 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:
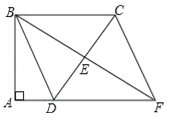
【題目】如圖,四邊形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是邊CD的中點,連接BE并延長與AD的延長線相交于點F.
(1)求證:四邊形BDFC是平行四邊形;
(2)若△BCD是等腰三角形,求四邊形BDFC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度數,下面給出了求∠AGD的度數的過程,將此補充完整并在括號里填寫依據. 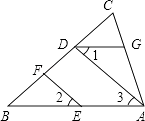
【解】∵EF∥AD(已知)
∴∠2=()
又∵∠1=∠2(已知)
∴∠1=∠3(等式性質或等量代換)
∴AB∥()
∴∠BAC+=180°()
又∵∠BAC=70°(已知)
∴∠AGD=110°(等式性質)
查看答案和解析>>
科目:初中數學 來源: 題型:
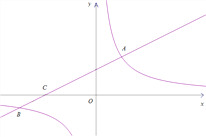
【題目】如圖,在平面直角坐標系xOy中,直線![]() 與雙曲線
與雙曲線![]() 相交于點A(m,3),B(-6,n),與x軸交于點C.
相交于點A(m,3),B(-6,n),與x軸交于點C.
(1)求直線![]() 的解析式;
的解析式;
(2)若點P在x軸上,且![]() ,求點P的坐 標(直接寫出結果).
,求點P的坐 標(直接寫出結果).
查看答案和解析>>
科目:初中數學 來源: 題型:
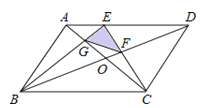
【題目】如圖,平行四邊形ABCD中,E是AD上的一點,且AE=![]() AD,對角線AC,BD交于點O,EC交BD于F,BE交AC于G,如果平行四邊形ABCD的面積為S,那么,△GEF的面積為( )
AD,對角線AC,BD交于點O,EC交BD于F,BE交AC于G,如果平行四邊形ABCD的面積為S,那么,△GEF的面積為( )
A. ![]() S B.
S B. ![]() S C.
S C. ![]() S D.
S D. ![]() S
S
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某機械廠加工車間有84名工人,平均每人每天加工大齒輪16個或者小齒輪10個,已知1個大齒輪與2個小齒輪剛好配成一套,問分別安排多少名工人加工大,小齒輪,才能使每天加工的大小齒輪剛好配套?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com