
 已知如圖等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于點D,點P是BA延長線上一點,點O是線段AD上一點,OP=OC,下面的結論:①∠APO+∠DCO=30°;②△OPC是等邊三角形;③AC=AO+AP;④S△ABC=S四邊形AOCP.其中正確的有________個.
已知如圖等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于點D,點P是BA延長線上一點,點O是線段AD上一點,OP=OC,下面的結論:①∠APO+∠DCO=30°;②△OPC是等邊三角形;③AC=AO+AP;④S△ABC=S四邊形AOCP.其中正確的有________個.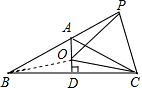 解:連接OB,
解:連接OB, ∠BAC=
∠BAC= ×120°=60°,
×120°=60°,
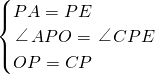 ,
,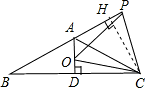 ∴AC=AE+CE=AO+AP;
∴AC=AE+CE=AO+AP; AB•CH,
AB•CH, AP•CH+
AP•CH+ OA•CD=
OA•CD= AP•CH+
AP•CH+ OA•CH=
OA•CH= CH•(AP+OA)=
CH•(AP+OA)= CH•AC,
CH•AC,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
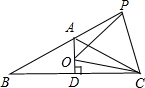 已知如圖等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于點D,點P是BA延長線上一點,點O是線段AD上一點,OP=OC,下面的結論:①∠APO+∠DCO=30°;②△OPC是等邊三角形;③AC=AO+AP;④S△ABC=S四邊形AOCP.其中正確的有( )個.
已知如圖等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于點D,點P是BA延長線上一點,點O是線段AD上一點,OP=OC,下面的結論:①∠APO+∠DCO=30°;②△OPC是等邊三角形;③AC=AO+AP;④S△ABC=S四邊形AOCP.其中正確的有( )個.查看答案和解析>>
科目:初中數學 來源: 題型:
 落在BC上D點,若△DCE和△FBD都是等腰三角形,
落在BC上D點,若△DCE和△FBD都是等腰三角形,查看答案和解析>>
科目:初中數學 來源: 題型:
已知:如圖,等腰梯形ABCD的邊BC在x軸上,點A在y軸的正方向上,A( 0, 6 ),D ( 4,6),且AB=![]() .
.
(1)求點B的坐標;
(2)求經過( )
A. B.D三點的拋物線的解析式;
(3)在(2)中所求的拋物線上是否存在一點P,使得S△ABC = ![]() S梯形ABCD ?若存在,請求出該點坐標,若不存在,請說明理由.
S梯形ABCD ?若存在,請求出該點坐標,若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com