Question

（10分）如圖，在單位長度為1的正方形網格中，一段圓弧經過網格的交點A、B、C．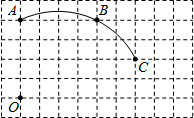

（1）請完成如下操作：
①以點O為原點、豎直和水平方向所在的直線為坐標軸、網格邊長為單位長，建立平面直角坐標系；②用直尺和圓規畫出該圓弧所在圓的圓心D的位置（不用寫作法，保留作圖痕跡），并連接AD、CD．
（2）請在（1）的基礎上，完成下列問題：
①寫出點的坐標：C      、D        ；
②⊙D的半徑=        .（ 結果保留根號）；
③若扇形ADC是一個圓錐的側面展開圖，求該圓錐的底面面積. （結果保留π）

Answer 1

（1）①建立平面直角坐標系；②找出圓心；
（2）①C（6，2）；D（2，0）；②OA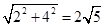＝；③∵OD＝CF，AD＝CD，∠AOD＝∠CFD＝90°，∴△AOD≌△DFC，∴∠OAD＝∠CDF，∵∠OAD＋∠ADO＝90°，∴∠ADO＋∠CDF＝90°，∴∠ADC＝90°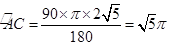，∴，∴該圓錐的底面半徑為：，∴該圓錐的底面面積為：．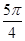

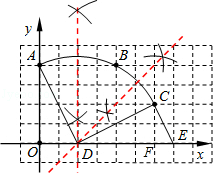
解析（1）根據敘述，利用正方形的網格即可作出坐標軸；
（2）①利用（1）中所作的坐標系，即可表示出點的坐標；
②在Rt△OAD中，利用勾股定理即可求得半徑長；
③可以證得∠ADC=90°，利用扇形的面積公式即可求得扇形的面積．
考點：垂徑定理；勾股定理；直線與圓的位置關系；圓錐的計算；作圖—復雜作圖．
點評：本題主要考查了垂徑定理，圓錐的計算，正確求出弧長是難點．