【題目】在四張背面完全相同的紙牌A、B、C、D，其中正面分別畫有四個不同的幾何圖形（如圖），小華將這4張紙牌背面朝上洗勻后摸出一張，放回洗勻后再摸一張．
（1）用樹狀圖（或列表法）表示兩次摸牌所有可能出現的結果（紙牌可用A、B、C、D表示）；
（2）求摸出兩張紙牌牌面上所畫幾何圖形，既是軸對稱圖形又是中心對稱圖形的概率．
寒假樂園北京教育出版社系列答案科目：初中數學 來源： 題型：
【題目】某中學為打造書香校園，計劃購進甲、乙兩種規格的書柜放置新購進的圖書，調查發現，若購買甲種書柜3個、乙種書柜2個，共需資金1020元；若購買甲種書柜4個，乙種書柜3個，共需資金1440元．
（1）甲、乙兩種書柜每個的價格分別是多少元？
（2）若該校計劃購進這兩種規格的書柜共20個，其中乙種書柜的數量不少于甲種書柜的數量，學校至多能夠提供資金4320元，請設計幾種購買方案供這個學校選擇．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲，乙兩家汽車銷售公司根據近幾年的銷售量分別制作了如圖所示的統計圖，從2014～2018年，這兩家公司中銷售量增長較快的是_____公司(填“甲”或“乙”)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，如圖1，點
是直線
上一點，
，
，射線
平分
.
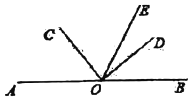
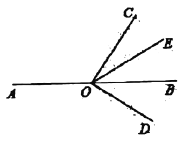
圖1 圖2
（1）求
的度數；
（2）將圖1中
按順時針方向轉至圖2所示的位置，仍然平分，
，則
___________.（用含有
的代數式表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，四邊形ABCD是正方形，點E是邊BC的中點，∠AEF＝90°，且EF交正方形ABCD的外角∠DCG的平分線CF于點F．
（1）如圖2，取AB的中點H，連接HE，求證：AE＝EF．
（2）如圖3，若點E是BC的延長線上（除C點外）的任意一點，其他條件不變結論“AE＝EF”仍然成立嗎？如果正確，寫出證明過程：如果不正確，請說明理由．
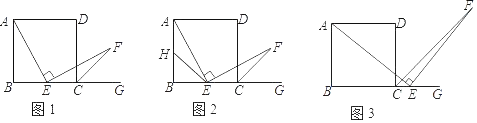
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，點D、E、F分別在邊AB、BC、CA上，且DE∥CA，DF∥BA．
下列四種說法：①四邊形AEDF是平行四邊形；②如果∠BAC=90°，那么四邊形AEDF是矩形；③如果AD平分∠BAC，那么四邊形AEDF是菱形；④如果AD⊥BC且AB=AC，那么四邊形AEDF是菱形．
其中，正確的有（ ） 個．
A．1 B．2 C．3 D．4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】
（1）如圖1，在正方形ABCD中，M是BC邊（不含端點B、C）上任意一點，P是BC延長線上一點，N是∠DCP的平分線上一點．若∠AMN=90°，求證：AM=MN．
下面給出一種證明的思路，你可以按這一思路證明，也可以選擇另外的方法證明．
證明：在邊AB上截取AE=MC，連ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE．
（下面請你完成余下的證明過程）
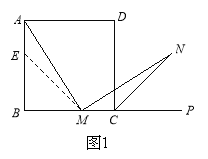
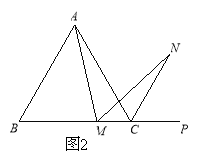
（2）若將（1）中的“正方形ABCD”改為“正三角形ABC”（如圖2），N是∠ACP的平分線上一點，則當∠AMN=60°時，結論AM=MN是否還成立？請說明理由．
（3）若將（1）中的“正方形ABCD”改為“正
邊形ABCD……X”，請你作出猜想：當∠AMN= °時，結論AM=MN仍然成立．（直接寫出答案，不需要證明）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
