
甲、乙兩個港口相距72千米,一艘輪船從甲港出發,順流航行3小時到達乙港,休息1小時后立即返回;一艘快艇在輪船出發2小時后從乙港出發,逆流航行2小時到甲港,并立即返回(掉頭時間忽略不計)。已知水流速度是2千米/時,下圖表示輪船和快艇距甲港的距離y(千米)與輪船出發時間x(小時)之間的函數關系式,結合圖象解答下列問題:
(順流速度=船在靜水中速度+水流速度;逆流速度=船在靜水中速度-水流速度)
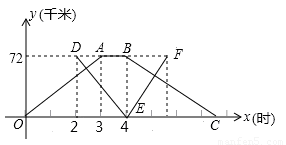
(1)輪船在靜水中的速度是 千米/時;快艇在靜水中的速度是 千米/時;
(2)求快艇返回時的解析式,寫出自變量取值范圍;
(3)快艇出發多長時間,輪船和快艇在返回途中相距12千米?(直接寫出結果)
(1)22 ; 38(2)y=40x-160(4≤x≤5.8)(3)3小時或3.4小時
【解析】解:(1)22 ; 38。
(2)點F的橫坐標為:4+72÷(38+2)=5.8 。
∴F(5.8,72),E(4,0)。
設EF解析式為y=kx+b(k≠0),則
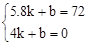 ,解得
,解得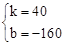 。
。
∴y=40x-160(4≤x≤5.8)。
(3)快艇出發3小時或3.4小時兩船相距12千米。
(1)輪船在靜水中的速度的=順流速度-水流速度=72÷3-2=22千米/時;
快艇在靜水中的速度=逆流速度+水流速度=72÷3+2=38千米/時。
(2)輪船回來時的速度是靜水中的速度與水速的差,路程是兩港口之間的距離,因而可以求得會來是所用的時間,則C的坐標可以求得,然后利用待定系數法即可求得函數的解析式。
(3)再求出函數EF的解析式,根據返回途中相距12千米,即兩個函數的函數值的差是12,則可以列出方程,求得x的值:
輪船返回用時72÷(22-2)=3.6,∴點C的坐標為(7.6,0)。
設線段BC所在直線的解析式為y=kx+b,
∵經過點(4,72)(7.6,0),∴ ,解得:
,解得: 。
。
∴線段BC所在直線的解析式為:y=-20x+152。
根據題意得:40x-160-(-20x+152)=12或-20x+152-(40x-160)=12,
解得:x=5或x=5.4。
∵快艇在輪船出發2小時后從乙港出發,
∴快艇出發3小時或3.4小時兩船相距12千米。


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案 期末好成績系列答案
期末好成績系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
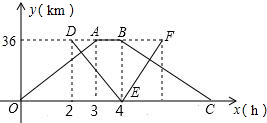 甲、乙兩個港口相距36千米,一艘輪船從甲港出發,順流航行3小時到達乙港.休息1小時后立即返回;一艘快艇在輪船出發2小時后從乙港出發,逆流航行2小時到達甲港,并立即返回(掉頭時間忽略不計).已知水流的速度是1千米/米.如圖表示輪船和快艇距甲港的距離y(千米)與輪船出發時間x(小時)之間的函數關系圖象.
甲、乙兩個港口相距36千米,一艘輪船從甲港出發,順流航行3小時到達乙港.休息1小時后立即返回;一艘快艇在輪船出發2小時后從乙港出發,逆流航行2小時到達甲港,并立即返回(掉頭時間忽略不計).已知水流的速度是1千米/米.如圖表示輪船和快艇距甲港的距離y(千米)與輪船出發時間x(小時)之間的函數關系圖象.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
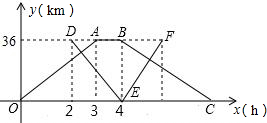 甲、乙兩個港口相距36千米,一艘輪船從甲港出發,順流航行3小時到達乙港.休息1小時后立即返回;一艘快艇在輪船出發2小時后從乙港出發,逆流航行2小時到達甲港,并立即返回(掉頭時間忽略不計).已知水流的速度是1千米/米.如圖表示輪船和快艇距甲港的距離y(千米)與輪船出發時間x(小時)之間的函數關系圖象.
甲、乙兩個港口相距36千米,一艘輪船從甲港出發,順流航行3小時到達乙港.休息1小時后立即返回;一艘快艇在輪船出發2小時后從乙港出發,逆流航行2小時到達甲港,并立即返回(掉頭時間忽略不計).已知水流的速度是1千米/米.如圖表示輪船和快艇距甲港的距離y(千米)與輪船出發時間x(小時)之間的函數關系圖象.查看答案和解析>>
科目:初中數學 來源:黑龍江省中考真題 題型:解答題

 速度是______千米/時;
速度是______千米/時;查看答案和解析>>
科目:初中數學 來源:2012年黑龍江省佳木斯市中考數學試卷(解析版) 題型:解答題
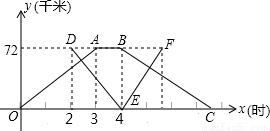
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com