
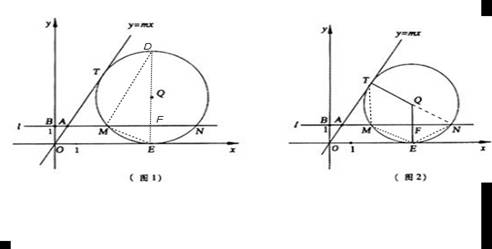
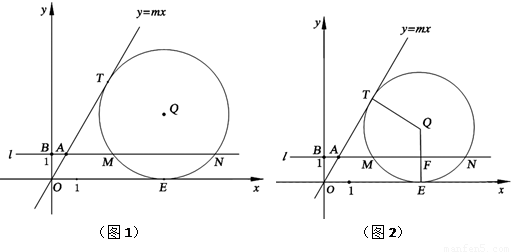
如圖1,在第一象限內(nèi),直線y=mx與過(guò)點(diǎn)B(0,1)且平行于x軸的直線l相交于點(diǎn)A,半徑為r的⊙Q與直線y=mx、x軸分別相切于點(diǎn)T、E,且與直線l分別交于不同的M、N兩點(diǎn).

(1)當(dāng)點(diǎn)A的坐標(biāo)為( ![]() ,p)時(shí),
,p)時(shí),
①填空:p=___ ,m= ___,∠AOE= ___.
②如圖2,連接QT、QE,QE交MN于點(diǎn)F,當(dāng)r=2時(shí),試說(shuō)明:以T、M、E、N為頂點(diǎn)的四邊形是等腰梯形;
(2)在圖1中,連接EQ并延長(zhǎng)交⊙Q于點(diǎn)D,試探索:對(duì)m、r的不同取值,經(jīng)過(guò)M、D、N三點(diǎn)的拋物線y=ax2+bx+c,a的值會(huì)變化嗎?若不變,求出a的值;若變化.請(qǐng)說(shuō)明理由.
解:(1)1, ![]() ,60°;
,60°;
(2)連接TM,ME,EN,ON,如圖,
∵OE和OP是⊙Q的切線,
∴QE⊥x軸,QT⊥OT,即∠QTA=90°,
而l∥x軸,
∴QE⊥MN,
∴MF=NF,
又∵當(dāng)r=2,EF=1,
∴QF=2-1=1,
∴四邊形QNEM為平行四邊形,即QN∥ME,
∴NQ=NE,即△QEN為等邊三角形,
∴∠NQE=60°,∠QNF=30°,
在四邊形OEQT中,∠QTO=∠QEO=90°,∠TOE=60°,
∴∠TQE=360°-90°-90°-60°=120°,
∴∠TQE+∠NQE=120°+60°=180°,
∴T、Q、N三點(diǎn)共線,即TN為直徑,
∴∠TMN=90°,
∴TN∥ME,
∴∠MTN=60°=∠TNE,
∴以T、M、E、N為頂點(diǎn)的四邊形是等腰梯形;
(3)對(duì)m、r的不同取值,經(jīng)過(guò)M、D、N三點(diǎn)的拋物線y=ax2+bx+c,a的值不會(huì)變化.理由如下:
連DM,ME,如圖,
∵DM為直徑,
∴∠DME=90°,
而DM垂直平分MN,
∴Rt△MFD∽R(shí)t△EFM,
∴MF2=EF•FD,
設(shè)D(h,k),(h>0,k=2r),則過(guò)M、D、N三點(diǎn)的拋物線的解析式為:y=a(x-h)2+k,
又∵M(jìn)、N的縱坐標(biāo)都為1,
當(dāng)y=1,a(x-h)2+k=1,解得x1=h-![]() , x2=h+
, x2=h+![]() ,
,
∴MN=2 ![]() ,
,
∴MF= ![]() MN=
MN=![]() ,
,
∴( ![]() )2=1•(k-1),
)2=1•(k-1),
∵k>1,
∴ ![]() =k-1,
=k-1,
∴a=-1.
解析:略


 世紀(jì)百通主體課堂小學(xué)課時(shí)同步達(dá)標(biāo)系列答案
世紀(jì)百通主體課堂小學(xué)課時(shí)同步達(dá)標(biāo)系列答案 世紀(jì)百通優(yōu)練測(cè)系列答案
世紀(jì)百通優(yōu)練測(cè)系列答案 百分學(xué)生作業(yè)本題練王系列答案
百分學(xué)生作業(yè)本題練王系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
| ||
| 3 |
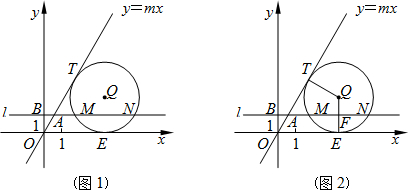
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
P點(diǎn)為拋物線![]() (
(![]() 為常數(shù),
為常數(shù),![]() )上任一點(diǎn),將拋物線繞頂點(diǎn)
)上任一點(diǎn),將拋物線繞頂點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() 后得到的新圖象與
后得到的新圖象與![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的上方),點(diǎn)
的上方),點(diǎn)![]() 為點(diǎn)
為點(diǎn)![]() 旋轉(zhuǎn)后的對(duì)應(yīng)點(diǎn).
旋轉(zhuǎn)后的對(duì)應(yīng)點(diǎn).

1.(1)當(dāng)![]() ,點(diǎn)
,點(diǎn)![]() 橫坐標(biāo)為4時(shí),求
橫坐標(biāo)為4時(shí),求![]() 點(diǎn)的坐標(biāo);
點(diǎn)的坐標(biāo);
2.(2)設(shè)點(diǎn)![]() ,用含
,用含![]() 、
、![]() 的代數(shù)式表示
的代數(shù)式表示![]() ;
;
3.(3) 如圖,點(diǎn)![]() 在第一象限內(nèi), 點(diǎn)
在第一象限內(nèi), 點(diǎn)![]() 在
在![]() 軸的正半軸上,點(diǎn)
軸的正半軸上,點(diǎn)![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 平分
平分![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時(shí),求
時(shí),求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2013年廣東省深圳市中考數(shù)學(xué)模擬試卷(五)(解析版) 題型:解答題
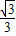 ,p)時(shí),
,p)時(shí),查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2012年福建省泉州市中考數(shù)學(xué)試卷(樣卷)(解析版) 題型:解答題
 ,p)時(shí),
,p)時(shí),查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年福建省泉州市九年級(jí)升學(xué)考試(樣卷)數(shù)學(xué)試卷(解析版) 題型:解答題
如圖1,在第一象限內(nèi),直線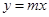 與過(guò)點(diǎn)
與過(guò)點(diǎn) 且平行于
且平行于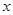 軸的直線
軸的直線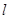 相交于點(diǎn)
相交于點(diǎn)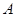 ,半徑為
,半徑為 的⊙
的⊙ 與直線
與直線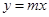 、
、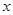 軸分別相切于點(diǎn)
軸分別相切于點(diǎn) 、
、 ,且與直線
,且與直線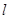 分別交于不同的
分別交于不同的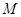 、
、 兩點(diǎn).
兩點(diǎn).
(1)當(dāng)點(diǎn)A的坐標(biāo)為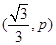 時(shí),
時(shí),
① 填空: = ,
= , = ,
= ,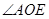 = ;
= ;
②如圖2,連結(jié)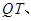
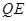 ,
,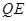 交直線
交直線 于
于 ,當(dāng)
,當(dāng)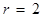 時(shí),試說(shuō)明以
時(shí),試說(shuō)明以 、
、
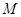 、
、 、
、 為頂點(diǎn)的四邊形是等腰梯形;
為頂點(diǎn)的四邊形是等腰梯形;
(2)在圖1中,連結(jié)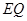 并延長(zhǎng)交⊙
并延長(zhǎng)交⊙ 于點(diǎn)
于點(diǎn) ,試探索:對(duì)不同的
,試探索:對(duì)不同的 取值,經(jīng)過(guò)
取值,經(jīng)過(guò)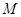 、
、 、
、 三點(diǎn)的拋物線
三點(diǎn)的拋物線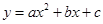 ,
,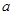 的值會(huì)變化嗎?若不變,求出
的值會(huì)變化嗎?若不變,求出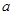 的值;若變化,請(qǐng)說(shuō)明理由.
的值;若變化,請(qǐng)說(shuō)明理由.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com