
【題目】如圖,直線y=![]() x+
x+![]() 與x軸交于點A,與y軸交于點C,以AC為直徑作⊙M,點D是劣弧AO上一動點(D點與A,C不重合).拋物線y=-
與x軸交于點A,與y軸交于點C,以AC為直徑作⊙M,點D是劣弧AO上一動點(D點與A,C不重合).拋物線y=-![]() x+bx+c經過點A、C,與x軸交于另一點B,
x+bx+c經過點A、C,與x軸交于另一點B,
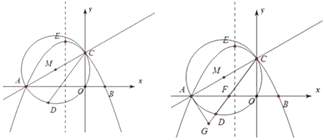
(1)求拋物線的解析式及點B的坐標;
(2)在拋物線的對稱軸上是否存在一點P,是︱PA—PC︱的值最大;若存在,求出點P的坐標;若不存在,請說明理由。
(3)連CD交AO于點F,延長CD至G,使FG=2,試探究當點D運動到何處時,直線GA與⊙M相切,并請說明理由.
【答案】(1)y=![]() , B(1,0) ;(2)見解析;(3)見解析.
, B(1,0) ;(2)見解析;(3)見解析.
【解析】(1)直接利用待定系數法求二次函數解析式,進而求出其對稱軸和B點坐標;
(2)首先利用待定系數法求一次函數解析式進而得出,此時PA=PB,|PA-PC|的值最大,求出即可;
(3)當D運動到劣弧AO的中點時,直線AG與⊙M相切,利用已知得出△AFG為等邊三角形,進而求出∠CAG=30°+60°=90°,即可得出答案.
(1)由y=![]() x+
x+![]() , 得:A(-3,0),C(0,
, 得:A(-3,0),C(0,![]() ),
),
將其代入拋物線解析式得:![]() ,解得:
,解得: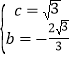 ,
,
∴y=![]() ,
,
∵對稱軸是x=-1,
∴由對稱性得B(1,0);
(2)延長BC與對稱軸的交點就是點P,
設直線BC的解析式為y=mx+n,
把B(1,0),C(0,![]() )代入得:
)代入得:![]() ,解得:
,解得:![]() ,
,
則直線BC解析式為:y=-![]() x+
x+![]() ,
,
當x=-1時,y=2![]() ,
,
∴P(-1, 2![]() );
);
(3)結論:當D運動到劣弧AO的中點時,直線AG與⊙M相切,理由如下:
∵在RT△AOC中,tan∠CAO=![]() ,
,
∴∠CAO=30°,∠ACO=60°,
∵點D是![]() 的中點,
的中點,
∴![]() ,
,
∴∠ACD=∠DCO=30°,
∴OF=OCtan30°=1,∠CF O=60°,
∴△AFG中,AF=3-1=2,∠AFG=∠CFO=60°,
∵FG=2,
∴△AFG為等邊三角形,
∴∠GAF=60°,
∴∠CAG=30°+60°=90°,
∴AC⊥AG,
∴AG為⊙M的切線.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:初中數學 來源: 題型:
【題目】小明所在的學校加強學生的體育鍛煉,準備從某體育用品商店一次購買若干個足球和籃球(每個足球的價格相同,每個籃球的價格相同),若購買2個籃球和3個足球共需310元,購買5個籃球和2個足球共需500元.
(1)每個籃球和足球各需多少元?
(2)根據實際情況,需從該商店一次性購買籃球和足球功60個,要求購買籃球和足球的總費用不超過4000元,那么最多可以購買多少個籃球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰直角三角形![]() 中,
中,![]() ,
,![]() .先將
.先將![]() 繞點
繞點![]() 逆時針方向旋轉
逆時針方向旋轉![]() ,得到
,得到![]() ,點
,點![]() 對應點
對應點![]() ,點
,點![]() 對應點
對應點![]() ;再將
;再將![]() 沿
沿![]() 方向平移,得到
方向平移,得到![]() ,點
,點![]() 、
、![]() 、
、![]() 的對應點分別是點
的對應點分別是點![]() 、
、![]() 、
、![]() ,設平移的距離為
,設平移的距離為![]() ,且
,且![]() .
.
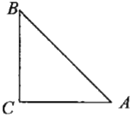
(1)在圖中畫出![]() 和
和![]() ;
;
(2)記![]() 與
與![]() 的交點為點
的交點為點![]() ,
,![]() 與
與![]() 的交點為點
的交點為點![]() ,如果四邊形
,如果四邊形![]() 的面積是
的面積是![]() 的面積的3倍,試求四邊形
的面積的3倍,試求四邊形![]() 和
和![]() 的面積的比值.
的面積的比值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中:
①0是最小的整數;
②有理數不是正數就是負數;
③正整數、負整數、正分數、負分數統稱為有理數;
④非負數就是正數;
⑤![]() 不僅是有理數,而且是分數;
不僅是有理數,而且是分數;
⑥![]() 是無限不循環小數,所以不是有理數;
是無限不循環小數,所以不是有理數;
⑦無限小數不都是有理數;
⑧正數中沒有最小的數,負數中沒有最大的數.
其中錯誤的說法的個數為( )
A.7個B.6個C.5個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形![]() 為正方形.在邊
為正方形.在邊![]() 上取一點
上取一點![]() ,連接
,連接![]() ,使
,使![]() .
.
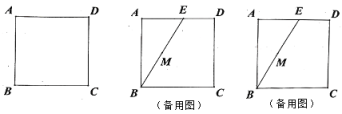
(1)利用尺規作圖(保留作圖痕跡):分別以點![]() 、
、![]() 為圓心,
為圓心,![]() 長為半徑作弧交正方形內部于點
長為半徑作弧交正方形內部于點![]() ,連接
,連接![]() 并延長交邊
并延長交邊![]() 于點
于點![]() ,則
,則![]() ;
;
(2)在前面的條件下,取![]() 中點
中點![]() ,過點
,過點![]() 的直線分別交邊
的直線分別交邊![]() 、
、![]() 于點
于點![]() 、
、![]() .
.
①當![]() 時,求證:
時,求證:![]() ;
;
②當![]() 時,延長
時,延長![]() ,
,![]() 交于
交于![]() 點,猜想
點,猜想![]() 與
與![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在郴州市的日常工作中,灑水車每天都在國慶路上來回灑水.我們約定灑水車在行駛過程中,向北的行程記為正數,向南的行程記為負數.2017年8月20日這一天,某臺灑水車市政工程處出發,所走的路程(單位:千米)為:+5,+7.5,-8,-3,+9.5,+2.5,-11,-3.5.問:
(1)這天收工時,這臺灑水車離市政工程處多遠?它在市政工程處的南邊還是北邊?
(2)若灑水車每走1千米耗油0.2升,請問這一天這臺灑水車在灑水過程中耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
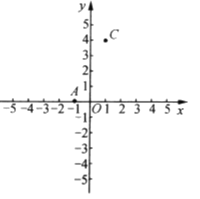
【題目】如圖,![]() ,
,![]() ,點
,點![]() 在
在![]() 軸上,且
軸上,且![]() .
.
(1)求點![]() 的坐標,并畫出
的坐標,并畫出![]() ;
;
(2)求![]() 的面積;
的面積;
(3)在![]() 軸上是否存在點
軸上是否存在點![]() ,使以
,使以![]() 三點為頂點的三角形的面積為10?若存在,請直接寫出點
三點為頂點的三角形的面積為10?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD為△ABC外接圓⊙O的直徑,且∠BAE=∠C.
(1)求證:AE與⊙O相切于點A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的長.
,求AD的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com