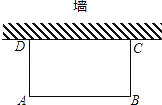
【題目】如圖，利用一面墻(墻的長度不超過45m)，用80m長的籬笆圍一個矩形場地．
(1)怎樣圍才能使矩形場地的面積為750m2？
(2)能否使所圍矩形場地的面積為810m2 ，為什么？
【答案】⑴圍成矩形長為30m，寬為25 m時，能使矩形面積為750㎡。
⑵不能。
【解析】
試題（1）設所圍矩形ABCD的長AB為x米，則寬AD為
米，根據矩形面積的計算方法列出方程求解；（2）假使矩形面積為810米，則方程無實數根，所以不能圍成矩形場地．
試題解析：（1）設所圍矩形ABCD的長AB為x米，則寬AD為米．
依題意，得
，即
.
解此方程，得x1=30，x2=50.
∵墻的長度不超過45m，∴x2=50不合題意，應舍去．
當x=30時，
.
答：當所圍矩形的長為30m、寬為25m時，能使矩形的面積為750m2．
（2）不能．理由如下：
由
得
．
∵
，
∴方程沒有實數根．
∴不能使所圍矩形場地的面積為810m2．
名校課堂系列答案科目：初中數學 來源： 題型：
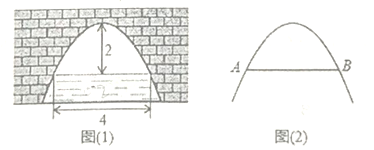
【題目】如圖（1）是一個橫斷面為拋物線形狀的拱橋，當水面寬
為
時，拱頂與水面距離為
.
（1）請你在圖（2）中，建立適當的平面直角坐標系，使該拋物線拱橋的函數關系式符合
形式，并求此時，函數關系式；
（2）當水面上升
時，求水面寬度.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線y＝ax2+bx+c（a≠0）的對稱軸為直線x＝﹣2，與x軸的一個交點在（﹣3，0）和（﹣4，0）之間，其部分圖象如圖所示，則下列結論：①4a﹣b＝0；②c＜0；③﹣3b+4c＞0；④4a﹣2b≥at2+bt（t為實數）；⑤點（﹣
，y1），（﹣
，y2），（﹣
，y3）是該拋物線上的點，則y1＜y2＜y3，其中正確的結論有（ ）
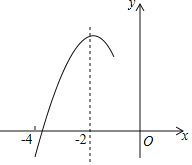
A. ②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AD平分∠BAC，AB=AC，連接BC，交AD于點E，下列說法正確的有（ ）
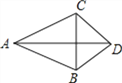
①∠BAC=∠ACB；②S四邊形ABDC=ADCE；③AB2+CD2=AC2+BD2；④AB﹣BD=AC﹣CD．
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
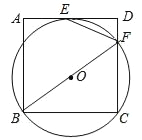
【題目】如圖，過正方形ABCD頂點B，C的⊙O與AD相切于點E，與CD相交于點F，連接EF．
（1）求證：EF平分∠BFD．
（2）若tan∠FBC＝
，DF＝
，求EF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某旅行社推出一條成本價為500元/人的省內旅游線路.游客人數
（人/月）與旅游報價
（元/人）之間的關系為
，已知：旅游主管部門規定該旅游線路報價在800元/人～1200元/人之間.
（1）要將該旅游線路每月游客人數控制在200人以內，求該旅游線路報價的取值范圍；
（2）求經營這條旅游線路每月所需要的最低成本；
（3）當這條旅游線路的旅游報價為多少時，可獲得最大利潤？最大利潤是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某文具店購進一批紀念冊，每本進價為20元，出于營銷考慮，要求每本紀念冊的售價不低于20元且不高于28元，在銷售過程中發現該紀念冊每周的銷售量y（本）與每本紀念冊的售價x（元）之間滿足一次函數關系：當銷售單價為22元時，銷售量為36本；當銷售單價為24元時，銷售量為32本．
（1）求出y與x的函數關系式；
（2）當文具店每周銷售這種紀念冊獲得150元的利潤時，每本紀念冊的銷售單價是多少元？
（3）設該文具店每周銷售這種紀念冊所獲得的利潤為w元，將該紀念冊銷售單價定為多少元時，才能使文具店銷售該紀念冊所獲利潤最大？最大利潤是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
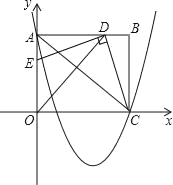
【題目】如圖，在平面直角坐標系中，矩形OABC的邊OA在y軸的正半軸上，C在x軸的正半軸上，已知A（0，8）、C（10，0），作∠AOC的平分線交AB于點D，連接CD，過點D作DE⊥CD交OA于點E．
（1）求點D的坐標；
（2）求證：△ADE≌△BCD；
（3）拋物線y＝
x2﹣
x+8經過點A、C，連接AC．探索：若點P是x軸下方拋物線上一動點，過點P作平行于y軸的直線交AC于點M．是否存在點P，使線段MP的長度有最大值？若存在，求出點P的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠C=90°，以AC為直徑作⊙O，交AB于D，過點O作OE∥AB，交BC于E．
（1）求證：ED為⊙O的切線；
（2）如果⊙O的半徑為
，ED=2，延長EO交⊙O于F，連接DF、AF，求△ADF的面積．
【答案】（1）證明見解析；（2）
【解析】試題分析：（1）首先連接OD，由OE∥AB，根據平行線與等腰三角形的性質，易證得
≌
即可得
，則可證得
為
的切線；
（2）連接CD，根據直徑所對的圓周角是直角，即可得
利用勾股定理即可求得
的長，又由OE∥AB，證得
根據相似三角形的對應邊成比例，即可求得
的長，然后利用三角函數的知識，求得
與
的長，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．
試題解析：(1)證明：連接OD，
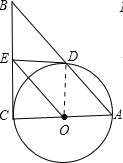
∵OE∥AB，
∴∠COE=∠CAD，∠EOD=∠ODA，
∵OA=OD,
∴∠OAD=∠ODA，
∴∠COE=∠DOE，
在△COE和△DOE中，
∴△COE≌△DOE(SAS)，
∴ED⊥OD，
∴ED是的切線；
(2)連接CD，交OE于M，
在Rt△ODE中，
∵OD=32，DE=2，
∵OE∥AB，
∴△COE∽△CAB，
∴AB=5，
∵AC是直徑，
∵EF∥AB，
∴S△ADF=S梯形ABEFS梯形DBEF
∴△ADF的面積為
【題型】解答題
【結束】
25
【題目】【題目】已知，拋物線y=ax2+ax+b（a≠0）與直線y=2x+m有一個公共點M（1，0），且a＜b．
（1）求b與a的關系式和拋物線的頂點D坐標（用a的代數式表示）；
（2）直線與拋物線的另外一個交點記為N，求△DMN的面積與a的關系式；
（3）a=﹣1時，直線y=﹣2x與拋物線在第二象限交于點G，點G、H關于原點對稱，現將線段GH沿y軸向上平移t個單位（t＞0），若線段GH與拋物線有兩個不同的公共點，試求t的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com