
【題目】如圖,經(jīng)過原點的拋物線![]() 與直線
與直線![]() 交于
交于![]() ,
,![]() 兩點,其對稱軸是直線
兩點,其對稱軸是直線![]() ,拋物線與
,拋物線與![]() 軸的另一個交點為
軸的另一個交點為![]() ,線段
,線段![]() 與
與![]() 軸交于點
軸交于點![]() .
.
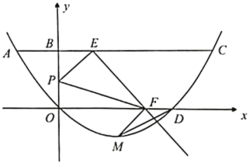
(1)求拋物線的解析式,并寫出點![]() 的坐標(biāo);
的坐標(biāo);
(2)若點![]() 為線段
為線段![]() 上一點,且
上一點,且![]() ,點
,點![]() 為線段
為線段![]() 上不與端點重合的動點,連接
上不與端點重合的動點,連接![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線交
的垂線交![]() 軸于點
軸于點![]() ,連接
,連接![]() ,探究在
,探究在![]() 點運動過程中,線段
點運動過程中,線段![]() ,
,![]() 有何數(shù)量關(guān)系?并證明所探究的結(jié)論;
有何數(shù)量關(guān)系?并證明所探究的結(jié)論;
(3)設(shè)拋物線頂點為![]() ,求當(dāng)
,求當(dāng)![]() 為何值時,
為何值時,![]() 為等腰三角形?
為等腰三角形?
【答案】(1)![]() ;點
;點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ;(2)
;(2)![]() ,理由見解析;(3)
,理由見解析;(3)![]() 或
或![]()
【解析】
(1)先求出a、b的值,然后求出解析式,再求出點D的坐標(biāo)即可;
(2)由題意,先求出點E的坐標(biāo),然后證明![]() ,得到
,得到![]() ,結(jié)合勾股定理,即可得到答案;
,結(jié)合勾股定理,即可得到答案;
(3)根據(jù)題意,可分為三種情況進行![]() 或
或![]() 或
或![]() ,分別求出三種情況的值即可.
,分別求出三種情況的值即可.
解:(1)∵拋物線![]() 經(jīng)過原點,
經(jīng)過原點,
∴![]() .
.
又拋物線的對稱軸是直線![]() ,
,
∴![]() ,解得:
,解得:![]() .
.
∴拋物線的解析式為:![]() .
.
令![]() ,
,
解得:![]() ,
,![]() .
.
∴點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
(2)線段![]() 、
、![]() 的數(shù)量關(guān)系為:
的數(shù)量關(guān)系為:![]() .
.
證明:由拋物線的對稱性得線段![]() 的中點為
的中點為![]() ,
,
如圖①,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
過點![]() 作
作![]() 軸于
軸于![]() ,則
,則![]() .
.

∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
在![]() 與
與![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() .
.
(3)由![]() ,
,
∴頂點![]() 坐標(biāo)為
坐標(biāo)為![]() .
.
若![]() 為等腰三角形,可能有三種情形:
為等腰三角形,可能有三種情形:
(I)若![]() .如圖②所示:
.如圖②所示:
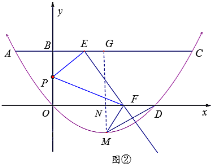
連接![]() 交
交![]() 軸于點
軸于點![]() ,則
,則![]() ,
,
∵![]() ,
,
∴![]() .
.
設(shè)![]() ,則
,則![]() .
.
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,即點M的縱坐標(biāo)為
,即點M的縱坐標(biāo)為![]() ;
;
令![]() ,則
,則![]() ,
,
∴![]() ,即ON=2,
,即ON=2,
∴OF=![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△OPF中,由勾股定理,得
![]() ,
,
∴![]() ,
,
∴![]() .
.
(II)若![]() .如圖③所示:
.如圖③所示:

此時![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(I)知,![]() ,
,![]() ,
,
在Rt△OPF中,由勾股定理,得
![]() ,
,
∴![]()
∴![]() .
.
(III)若![]() .由拋物線對稱性可知,此時點
.由拋物線對稱性可知,此時點![]() 與原點
與原點![]() 重合.
重合.
∵![]() ,點
,點![]() 在直線
在直線![]() 上方,與點
上方,與點![]() 在線段
在線段![]() 上運動相矛盾,
上運動相矛盾,
故此種情形不存在.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在平面直角坐標(biāo)系中,拋物線y=﹣![]() x+3與x軸的一個交點為點A,與y軸的交點為點B,拋物線的對稱軸l與x軸交于點,與線段AB交于點E,點D是對稱軸l上一動點.
x+3與x軸的一個交點為點A,與y軸的交點為點B,拋物線的對稱軸l與x軸交于點,與線段AB交于點E,點D是對稱軸l上一動點.
(1)點A的坐標(biāo)是 ,點B的坐標(biāo)是 ;
(2)是否存在點D,使得△BDE和△ACE相似?若存在,請求出點D的坐標(biāo),若不存在,請說明理由;
(3)如圖2,拋物線的對稱軸l向右平移與線段AB交于點F,與拋物線交于點G,當(dāng)四邊形DEFG是平行四邊形且周長最大時,求出點G的橫坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù)![]() (其中
(其中![]() )的圖像與
)的圖像與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
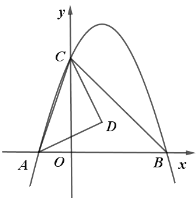
(1)點![]() 的坐標(biāo)為 ,
的坐標(biāo)為 ,![]()
![]() ;
;
(2)若![]() 為
為![]() 的外心,且
的外心,且![]() 與
與![]() 的面積之比為
的面積之比為![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,試探究拋物線![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ,若存在,求出點
,若存在,求出點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】四邊形ABCD是正方形,PA是過正方形頂點A的直線,作DE⊥PA于E,將射線DE繞點D逆時針旋轉(zhuǎn)45°與直線PA交于點F.
(1)如圖1,當(dāng)∠PAD=45°時,點F恰好與點A重合,則![]() 的值為 ;
的值為 ;
(2)如圖2,若45°<∠PAD<90°,連接BF、BD,試求![]() 的值,并說明理由.
的值,并說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
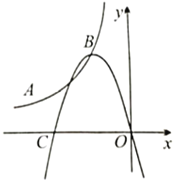
【題目】如圖,在平面直角坐標(biāo)系![]() 中,反比例函數(shù)
中,反比例函數(shù)![]()
![]() 的圖象經(jīng)過點
的圖象經(jīng)過點![]() 與點
與點![]() ,拋物線
,拋物線![]() 經(jīng)過原點
經(jīng)過原點![]() ,頂點是
,頂點是![]() ,且與
,且與![]() 軸交于另一點
軸交于另一點![]() ,則
,則![]() _________.
_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為實現(xiàn)區(qū)域教育均衡發(fā)展,我市計劃對某縣![]() 、
、![]() 兩類薄弱學(xué)校全部進行改造.根據(jù)預(yù)算,共需資金1575萬元.改造一所
兩類薄弱學(xué)校全部進行改造.根據(jù)預(yù)算,共需資金1575萬元.改造一所![]() 類學(xué)校和兩所
類學(xué)校和兩所![]() 類學(xué)校共需資金230萬元;改造兩所
類學(xué)校共需資金230萬元;改造兩所![]() 類學(xué)校和一所
類學(xué)校和一所![]() 類學(xué)校共需資金205萬元.
類學(xué)校共需資金205萬元.
(1)改造一所![]() 類學(xué)校和一所
類學(xué)校和一所![]() 類學(xué)校所需的資金分別是多少萬元?
類學(xué)校所需的資金分別是多少萬元?
(2)若該縣的![]() 類學(xué)校不超過5所,則
類學(xué)校不超過5所,則![]() 類學(xué)校至少有多少所?
類學(xué)校至少有多少所?
(3)我市計劃今年對該縣![]() 、
、![]() 兩類學(xué)校共6所進行改造,改造資金由國家財政和地方財政共同承擔(dān).若今年國家財政撥付的改造資金不超過400萬元;地方財政投入的改造資金不少于70萬元,其中地方財政投入到
兩類學(xué)校共6所進行改造,改造資金由國家財政和地方財政共同承擔(dān).若今年國家財政撥付的改造資金不超過400萬元;地方財政投入的改造資金不少于70萬元,其中地方財政投入到![]() 、
、![]() 兩類學(xué)校的改造資金分別為每所10萬元和15萬元.請你通過計算求出有幾種改造方案?
兩類學(xué)校的改造資金分別為每所10萬元和15萬元.請你通過計算求出有幾種改造方案?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,
中,![]() 的頂點
的頂點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 軸的負(fù)半軸上,
軸的負(fù)半軸上,![]() ,
,![]() 在反比例函數(shù)
在反比例函數(shù)![]() (
(![]() )的圖象上,
)的圖象上,![]() 與
與![]() 軸交于點
軸交于點![]() ,且
,且![]() ,若
,若![]() 的面積是3,則
的面積是3,則![]() 的值是_________.
的值是_________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△EBF為等腰直角三角形,點B為直角頂點, 四邊形ABCD是正方形.
⑴ 求證:△ABE≌△CBF;
⑵ CF與AE有什么特殊的位置關(guān)系?請證明你的結(jié)論.
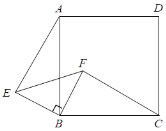
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩條輪船同時從港口A出發(fā),甲輪船以每小時30海里的速度沿著北偏東60°的方向航行,乙輪船以每小時15海里的速度沿著正東方向行進,1小時后,甲船接到命令要與乙船會合,于是甲船改變了行進的速度,沿著東南方向航行,結(jié)果在小島C處與乙船相遇.假設(shè)乙船的速度和航向保持不變,求:
(1)港口A與小島C之間的距離;
(2)甲輪船后來的速度.
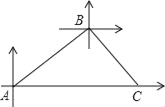
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com