
【題目】已知拋物線![]() :
:![]() 的項點為
的項點為![]() ,交
,交![]() 軸于
軸于![]() 、
、![]() 兩點(
兩點(![]() 點在
點在![]() 點左側),且
點左側),且![]() .
.
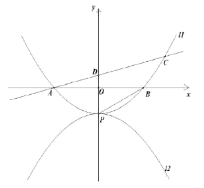
(1)求拋物線![]() 的函數解析式;
的函數解析式;
(2)過點![]() 的直線交拋物線于點
的直線交拋物線于點![]() ,交
,交![]() 軸于點
軸于點![]() ,若
,若![]() 的面積被
的面積被![]() 軸分為1: 4兩個部分,求直線
軸分為1: 4兩個部分,求直線![]() 的解析式;
的解析式;
(3)在(2)的情況下,將拋物線![]() 繞點
繞點![]() 逆時針旋轉180°得到拋物線
逆時針旋轉180°得到拋物線![]() ,點
,點![]() 為拋物線
為拋物線![]() 上一點,當點
上一點,當點![]() 的橫坐標為何值時,
的橫坐標為何值時,![]() 為直角三角形?
為直角三角形?
【答案】(1)![]() ;(2)直線
;(2)直線![]() 的解析式為
的解析式為![]() ;(3)點
;(3)點![]() 橫坐標為
橫坐標為![]() 或
或![]() 或
或![]() 或
或![]()
![]() 時,
時,![]() 為
為![]() .
.
【解析】
(1)求拋物線l1的頂點P(0,-2)得OP=2,由![]() 求得BP的長,進而求得OB即點B坐標,代入拋物線l1的解析式即求得a的值.
求得BP的長,進而求得OB即點B坐標,代入拋物線l1的解析式即求得a的值.
(2)求點A坐標為(-4,0),設直線AC解析式為y=kx+b,把點A代入得b=4k,所以能用k表示點D坐標,進而用k表示△AOD和△BOD的面積.把直線AC解析式與拋物線l1解析式聯立方程,即y相等時得到一個關于x的一元二次方程,解即為點A、C橫坐標,利用根與系數的關系求出點C橫坐標(用k表示),進而可用k表示C的縱坐標,再得到用k表示的△ABC面積.當k>0時,顯然S△AOD:S四邊形OBCD=1:4,即S△AOD=![]() S△ABC,故得到關于k的方程,求解即得k的值.當k<0,則得到的方程與k>0時相同,求得的k不滿足題意.綜合即求得直線AC的解析式.
S△ABC,故得到關于k的方程,求解即得k的值.當k<0,則得到的方程與k>0時相同,求得的k不滿足題意.綜合即求得直線AC的解析式.
(3)由于不確定點B、D、M哪個為直角頂點,故需分三種情況討論.設點M橫坐標為m,①若∠BDM=90°,過M作MN⊥y軸于點N,可證△BDO∽△DMN,用m表示MN、DN的長,代入相似三角形對應邊成比例即列得方程求m的值.②若∠DBM=90°,過點M作MQ⊥x軸于點Q,可證△BMQ∽△DBO,用m表示BQ、MQ的長,代入相似三角形對應邊成比例即列得方程求m的值.③若∠BMD=90°,則點M在以BD為直徑的圓除點B、D外的圓周上,但顯然以AB為直徑的圓與拋物線l2無交點,故此情況不存在滿足的m.
(1)當![]() 時,
時,![]()
∴頂點![]() ,
,![]()
∵![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]() ,代入拋物線
,代入拋物線![]() 得:
得:
![]() ,解得
,解得![]() ,
,
∴拋物線![]() 的函數解析式為
的函數解析式為![]()
(2)∵知拋物線![]() 交
交![]() 軸于
軸于![]() 、
、![]() 兩點
兩點
∴![]() 、
、![]() 關于
關于![]() 軸對稱,即
軸對稱,即![]()
∴![]()
設直線![]() 解析式:
解析式:![]() 點
點![]() 代入得:
代入得:![]()
∴![]()
∴直線![]() :
:![]() ,
,![]()
∴![]()
∵![]() ,整理得:
,整理得:![]()
∴![]()
∵![]()
∴![]() ,
,![]()
∴![]()
∴![]()
①若![]() ,則
,則![]()
∴![]()
∴![]()
解得:![]() (舍去),
(舍去),![]()
∴直線![]() 的解析式為
的解析式為![]()
②若![]() ,則
,則![]() ,
,![]()
∴![]() 解得:
解得:![]() (舍去),
(舍去),![]() (舍去)
(舍去)
綜上所述,直線![]() 的解析式為
的解析式為![]() .
.
(3)由(2)得:![]() ,
,![]()
∵拋物線![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到拋物線
得到拋物線![]()
∴拋物線![]() 解析式為:
解析式為:![]()
設點![]() 坐標為
坐標為![]()
①若![]() ,如圖1,則
,如圖1,則![]() 過
過![]() 作
作![]() 軸于點
軸于點![]()
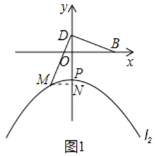
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]() ,即
,即![]()
∴![]()
解得:![]() ,
,![]()
②若![]() ,如圖2,過點
,如圖2,過點![]() 作
作![]() 軸于點
軸于點![]()
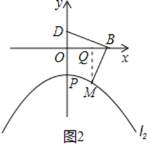
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]() ,即
,即![]()
∴![]() 解得:
解得:![]() ,
,![]()
③若![]() ,則點
,則點![]() 在以
在以![]() 為直徑的圓除點
為直徑的圓除點![]() 、
、![]() 外的圓周上
外的圓周上
顯然以![]() 為真徑的圓與拋物線
為真徑的圓與拋物線![]() 無交點,故此情況不存在滿足的
無交點,故此情況不存在滿足的![]()
綜上所述,點![]() 橫坐標為
橫坐標為![]() 或
或![]() 或
或![]() 或
或![]() 時,
時,![]() 為
為![]() .
.


科目:初中數學 來源: 題型:
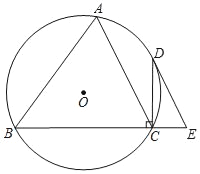
【題目】如圖,△ABC內接于⊙O,過點C作BC的垂線交⊙O于D,點E在BC的延長線上,且∠DEC=∠BAC.
(1)求證:DE是⊙O的切線;
(2)若AC∥DE,當AB=8,CE=2時,求⊙O直徑的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=![]() x+c與x軸交于點B(4,0),與y軸交于點C,拋物線y=
x+c與x軸交于點B(4,0),與y軸交于點C,拋物線y=![]() x2+bx+c經過點B,C,與x軸的另一個交點為點A.
x2+bx+c經過點B,C,與x軸的另一個交點為點A.
(1)求拋物線的解析式;
(2)點P是直線BC下方的拋物線上一動點,求四邊形ACPB的面積最大時點P的坐標;
(3)若點M是拋物線上一點,請直接寫出使∠MBC=![]() ∠ABC的點M的坐標.
∠ABC的點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD的一個角翻折,使得點D恰好落在BC邊上的點G處,折痕為EF,若EB為∠AEG的平分線,EF和BC的延長線交于點H.下列結論中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面積相等;⑤若![]() ,則
,則![]() .以上命題,正確的有( )
.以上命題,正確的有( )
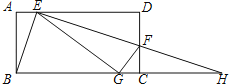
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
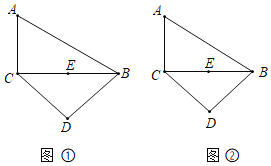
【題目】已知![]() 中,
中,![]() 點
點![]() 為
為![]() 的中點,以
的中點,以![]() 為底邊的等腰
為底邊的等腰![]() 按如圖所示位置擺放,且
按如圖所示位置擺放,且![]() .請僅用無刻度的直尺分別按下列要求作圖(保留作圖痕跡).
.請僅用無刻度的直尺分別按下列要求作圖(保留作圖痕跡).
![]() 如圖①,在
如圖①,在![]() 上求作一點
上求作一點![]() ,使四邊形
,使四邊形![]() 為菱形;
為菱形;
![]() 如圖②,過點
如圖②,過點![]() 作線段
作線段![]() 使得線段
使得線段![]() 將
將![]() 的面積平分.
的面積平分.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一個拋物線經過A(0,1),B(1,3),C(﹣1,1)三點.
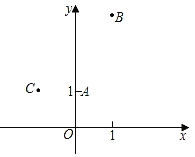
(1)求這個拋物線的表達式及其頂點D的坐標;
(2)聯結AB、BC、CA,求tan∠ABC的值;
(3)如果點E在該拋物線的對稱軸上,且以點A、B、C、E為頂點的四邊形是梯形,直接寫出點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
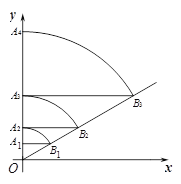
【題目】如圖,直線l:y=![]() x,點A1坐標為(0,1),過點A1作y軸的垂線交直線l于點B1,以原點O 為圓心,OB1長為半徑畫弧交y一軸于點A2;再過點A2作y軸的垂線交直線于點B2,以原點O為圓心,OB2長為半徑畫弧交y軸于點A3,…,按此做法進行下去,點A4的坐標為_______;點An的坐標為_______.
x,點A1坐標為(0,1),過點A1作y軸的垂線交直線l于點B1,以原點O 為圓心,OB1長為半徑畫弧交y一軸于點A2;再過點A2作y軸的垂線交直線于點B2,以原點O為圓心,OB2長為半徑畫弧交y軸于點A3,…,按此做法進行下去,點A4的坐標為_______;點An的坐標為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有大小兩種貨車,3輛大貨車與4輛小貨車一次可以運貨18噸,2輛大貨車與6輛小貨車一次可以運貨17噸.
(1)請問1輛大貨車和1輛小貨車一次可以分別運貨多少噸?
(2)目前有33噸貨物需要運輸,貨運公司擬安排大小貨車共計10輛,全部貨物一次運完,其中每輛大貨車一次運費花費130元,每輛小貨車一次運貨花費100元,請問貨運公司應如何安排車輛最節省費用?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在正六邊形![]() 中,有兩點
中,有兩點![]() 同時、同速從
同時、同速從![]() 中點
中點![]() 出發,P沿
出發,P沿![]() 方向運動,Q點沿
方向運動,Q點沿![]() 方向指向運動,10秒后,兩點與多邊形中心連線及多邊形(延長線)所圍成圖形的面積如圖(陰影部分的面積)有兩部分為
方向指向運動,10秒后,兩點與多邊形中心連線及多邊形(延長線)所圍成圖形的面積如圖(陰影部分的面積)有兩部分為![]() ,則
,則![]() 之間的數量關系是( )
之間的數量關系是( )
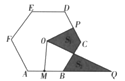
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com