
【題目】如圖,在![]() 中,點
中,點![]() 是線段
是線段![]() 上的動點,將線段
上的動點,將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到線段
得到線段![]() ,連接
,連接![]() .若已知
.若已知![]() ,設
,設![]() 兩點間的距離為
兩點間的距離為![]() 兩點間的距離為
兩點間的距離為![]() 兩點間的距離為
兩點間的距離為![]() .(若同學們打印的BC的長度如不是
.(若同學們打印的BC的長度如不是![]() ,請同學們重新畫圖、測量)
,請同學們重新畫圖、測量)
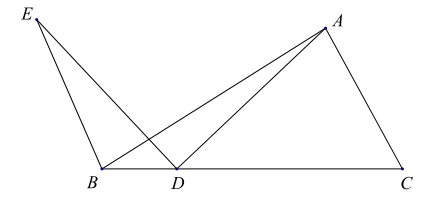
小明根據學習函數的經驗,分別對![]() 自變量x的變化而變化的規律進行了探究,下面是小明的探究過程,請補充完整:
自變量x的變化而變化的規律進行了探究,下面是小明的探究過程,請補充完整:
(1)按照下表中自變量![]() 的值進行取點、畫圖、測量,分別得到了
的值進行取點、畫圖、測量,分別得到了![]() 與
與![]() 的幾組對應值,如下表:
的幾組對應值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
|
| 5.66 | 4.32 |
| 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
寫出![]() 的值.(保留1位小數)
的值.(保留1位小數)
(2)在同一平面直角坐標系![]() 中,描出補全后的表中各組數值所對應的點
中,描出補全后的表中各組數值所對應的點![]() ,并畫出函數
,并畫出函數![]() 的圖象;
的圖象;
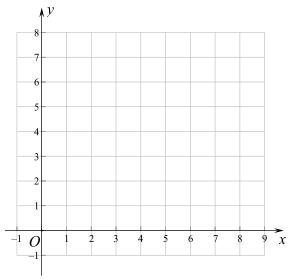
(3)結合函數圖像,解決問題:
①當![]() 在線段
在線段![]() 上時,
上時,![]() 的長度約為________
的長度約為________![]() ;
;
②當![]() 為等腰三角形時,
為等腰三角形時,![]() 的長度
的長度![]() 約為_______
約為_______![]() .
.
科目:初中數學 來源: 題型:
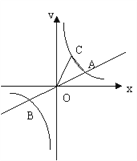
【題目】如圖,已知直線![]() 與雙曲線
與雙曲線![]() 交于A、B兩點,點B坐標為(-4,-2),C為雙曲線
交于A、B兩點,點B坐標為(-4,-2),C為雙曲線![]() 上一點,且在第一象限內,若△AOC面積為6,則點C坐標為( )
上一點,且在第一象限內,若△AOC面積為6,則點C坐標為( )
A. (4,2) B. (2,3) C. (3,4) D. (2,4)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC在直角坐標平面內,三個頂點的坐標分別為A(0,3)、B(3,4)、C(2,2)(正方形網格中每個小正方形的邊長是一個單位長度).
(1)畫出△ABC向下平移4個單位長度得到的△A1B1C1,點C1的坐標是 ;
(2)以點B為位似中心,在網格內畫出△A2B2C2,使△A2B2C2與△ABC位似,且位似比為2:1;
(3)四邊形AA2C2C的面積是 平方單位.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某植物園有一塊足夠大的空地,其中有一堵長為a米的墻,現準備用20米的籬笆圍兩間矩形花圃,中間用籬笆隔開.小俊設計了如圖甲和乙的兩種方案:
方案甲中AD的長不超過墻長;方案乙中AD的長大于墻長.
(1)若a=6.
①按圖甲的方案,要圍成面積為25平方米的花圃,則AD的長是多少米?
②按圖乙的方案,能圍成的矩形花圃的最大面積是多少?
(2)若0<a<6.5,哪種方案能圍成面積最大的矩形花圃?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
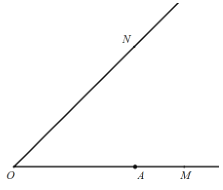
【題目】如圖,已知![]() ,
,![]() 為射線
為射線![]() 上一定點,點
上一定點,點![]() 關于射線
關于射線![]() 的對稱點為點
的對稱點為點![]() 為射線
為射線![]() 上一動點,連接
上一動點,連接![]() ,滿足
,滿足![]() 為鈍角,以點
為鈍角,以點![]() 為中心,將線段
為中心,將線段![]() 逆時針旋轉
逆時針旋轉![]() 至線段
至線段![]() ,滿足點
,滿足點![]() 在射線
在射線![]() 的反向延長線上.
的反向延長線上.
(1)依題意補全圖形;
(2)當點![]() 在運動過程中,旋轉角
在運動過程中,旋轉角![]() 是否發生變化?若不變化,請求出
是否發生變化?若不變化,請求出![]() 的值,若變化,請說明理由;
的值,若變化,請說明理由;
(3)從點![]() 向射線
向射線![]() 作垂線,與射線
作垂線,與射線![]() 的反向延長線交于點
的反向延長線交于點![]() ,探究線段
,探究線段![]() 和
和![]() 的數量關系并證明.
的數量關系并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
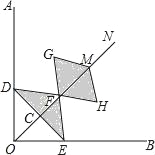
【題目】如圖,在Rt∠AOB的平分線ON上依次取點C,F,M,過點C作DE⊥OC,分別交OA,OB于點D,E,以FM為對角線作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,設OC=x,圖中陰影部分面積為y,則y與x之間的函數關系式是( )
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等腰△BCD中,∠DCB=120°,點E滿足∠DEC=60°.
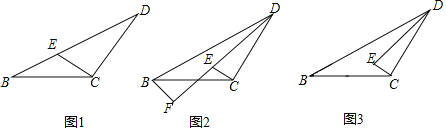
(1)如圖1,點E在邊BD上時,求證:ED=2BE;
(2)如圖2,過點B作DE的垂線交DE的延長線于點F,試探究DE和EF的數量關系,并證明;
(3)若∠DEB=150°,直接寫出BE,DE和EC的關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了堅持以人民為中心的發展思想,以不斷改善民生為發展的根本目的,某機構隨機對某小區部分居民進行了關于“社區服務工作滿意度”的調查,并根據調查結果繪制成如下不完整的統計圖表,根據圖標信息,解答下列問題:
滿意度 | 人數 | 所占百分比 |
非常滿意 | 12 |
|
滿意 | 54 |
|
比較滿意 |
|
|
不滿意 | 6 |
|
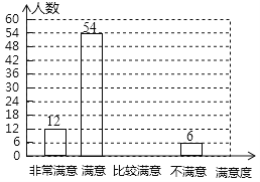
(1)本次調查的總人數為_______.
(2)請補全條形統計圖;
(3)據統計,該社區服務站平均每天接待居民約1000名,若將“非常滿意”和“消意”作為居民對社區服務站服務工作的肯定,請你估計該社區服務站服務工作平均每天得到多少名居民的肯定.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=a(x﹣![]() )(x+3)交x軸于點A、B,交y軸于點C,tan∠CAO=
)(x+3)交x軸于點A、B,交y軸于點C,tan∠CAO=![]() .
.
(1)求a值;
(2)點P為第一象限內拋物線上一點,點P的橫坐標為t,連接PA,PC,設△PAC的面積為S,求S與t之間的關系式;
(3)在(2)的條件下,點Q在第一象限內的拋物線上(點Q在點P的上方),過點P作PE⊥AB,垂足為E,點D在線段AQ上,點F在線段AO上連接ED、DF,DE交AP于點G,若∠QDF+∠QDE=180°,∠DFA+∠AED=90°,PG=PE,PG:EF=3:2,求點P的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com