
 已知拋物線C1的頂點為P(1,0),且過點(0,
已知拋物線C1的頂點為P(1,0),且過點(0, ).將拋物線C1向下平移h個單位(h>0)得到拋物線C2.一條平行于x軸的直線與兩條拋物線交于A、B、C、D四點(如圖),且點A、C關于y軸對稱,直線AB與x軸的距離是m2(m>0).
).將拋物線C1向下平移h個單位(h>0)得到拋物線C2.一條平行于x軸的直線與兩條拋物線交于A、B、C、D四點(如圖),且點A、C關于y軸對稱,直線AB與x軸的距離是m2(m>0). .
. )代入求出a的值,再化為一般形式即可;
)代入求出a的值,再化為一般形式即可; ),
), ,
, ,
, (x-1)2,
(x-1)2, x2-
x2- x+
x+ ;
; (x-1)2=4,
(x-1)2=4, (x-1)2-h,
(x-1)2-h, (-5-1)2-h=4,
(-5-1)2-h=4, (x-1)2=m2,
(x-1)2=m2, (x-1)2-h,
(x-1)2-h, (-1-2m-1)2-h=m2,
(-1-2m-1)2-h=m2,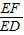 -
-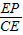 =
=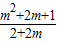 -
-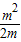 =
=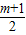 -
-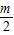 =
= ,
, .
.

 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案科目:初中數學 來源: 題型:
 (2013•株洲)已知拋物線C1的頂點為P(1,0),且過點(0,
(2013•株洲)已知拋物線C1的頂點為P(1,0),且過點(0,| 1 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知拋物線C1的頂點坐標是D(1,4),且經過點C(2,3),又與x軸交于點A、E(點A在點E左邊),與y軸交于點B.
如圖,已知拋物線C1的頂點坐標是D(1,4),且經過點C(2,3),又與x軸交于點A、E(點A在點E左邊),與y軸交于點B.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知拋物線C1的頂點為P(1,0),且過點(0,
已知拋物線C1的頂點為P(1,0),且過點(0, ).將拋物線C1向下平移h個單位(h>0)得到拋物線C2.一條平行于x軸的直線與兩條拋物線交于A、B、C、D四點(如圖),且點A、C關于y軸對稱,直線AB與x軸的距離是m2(m>0).
).將拋物線C1向下平移h個單位(h>0)得到拋物線C2.一條平行于x軸的直線與兩條拋物線交于A、B、C、D四點(如圖),且點A、C關于y軸對稱,直線AB與x軸的距離是m2(m>0). .
.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知拋物線C1的頂點坐標是D(1,4),且經過點C(2,3),又與x軸交于點A、E(點A在點E左邊),與y軸交于點B.
如圖,已知拋物線C1的頂點坐標是D(1,4),且經過點C(2,3),又與x軸交于點A、E(點A在點E左邊),與y軸交于點B.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com