已知關于x的一元二次方程x2+cx+a=0的兩個整數根恰好比方程x2+ax+b=0的兩個根都大1,求a+b+c的值.
【答案】
分析:設出第一個方程的兩根,表示出后面方程的另2根.利用根與系數的關系均得到與a的關系,進而消去a,得到兩個一次項的積為一個常數的形式,判斷可能的整數解,得到a,b,c的值,相加即可.
解答:解:設方程x
2+ax+b=0的兩個根為α,β,
∵方程有整數根,
設其中α,β為整數,且α≤β,
則方程x
2+cx+a=0的兩根為α+1,β+1,
∴α+β=-a,(α+1)(β+1)=a,(5分)
兩式相加,得αβ+2α+2β+1=0,
即(α+2)(β+2)=3,
∴

或
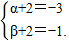
(10分)
解得
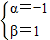
或
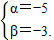
又∵a=-(α+β)=-[(-1)+1]=0,b=αβ=-1×1=-1,c=-[(α+1)+(β+1)]=-[(-1+1)+(1+1)]=-2,
或a=-(α+β)=-[(-5)+(-3)]=8,b=αβ=(-5)×(-3)=15,c=-[(α+1)+(β+1)]=-[(-5+1)+(-3+1)]=6,
∴a=0,b=-1,c=-2;或者a=8,b=15,c=6,
∴a+b+c=0+(-1)+(-2)=-3或a+b+c=8+15+6=29,
故a+b+c=-3,或29.(20分)
點評:主要考查一元二次方程根與系數關系的應用;利用根與系數的關系得到兩根之間的關系是解決本題的關鍵;消去a后得到兩個一次項的積為一個常數的形式是解決本題的難點.

 或
或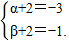 (10分)
(10分)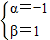 或
或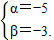


 .
. .
.