
.在△ABC中,∠C=90°,AC=4cm,BC=5cm,點D在BC上,并且CD=3cm,現有兩個動點P、Q分別從點A和點B同時出發,其中點P以1cm/s的速度,沿AC向終點C移動;點Q以1.25cm/s的速度沿BC向終點C移動.過點P作PE∥BC交AD于點E,連結EQ.設動點運動時間為x秒.
1.(1)用含x的代數式表示AE、DE的長度;
2.(2)當點Q在線段BD(不包括點B、D)上移動時,設△EDQ的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式,并寫出自變量
的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
3.(3)當![]() 為何值時,△EDQ為直角三角形.
為何值時,△EDQ為直角三角形.
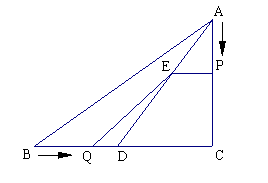
1.解:(1)在Rt△ADC中,∵AC=4,CD=3,
∴AD=5,
∵EP∥DC,
∴△AEP∽△ADC
![]()
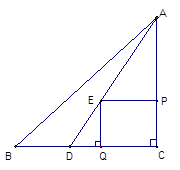
2.(2)∵BC=5,CD=3,∴BD=2
當點Q在BD上運動x秒后,DQ=2-1.25x,
則![]() ……………3
……………3
即y與x的函數解析式為:![]() ,
,
其中自變量的取值范圍是:0<x<1.6 ……………………3
3.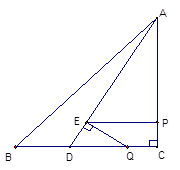 (3)分兩種情況討論:
(3)分兩種情況討論:
①當∠EQD=90°時,
∴EQ=PC=4-x,
∵EQ∥AC
∴△EDQ∽△ADC ……………………………4分
![]()
![]()
![]() ……………………5分
……………………5分
②當∠QED=90°時,
∵∠CDA=∠EDQ,∠QED=∠C=90°
∴△EDQ∽△CDA …………………………………6分
∴![]()
即
![]() ……………………7分
……………………7分
綜上所述,當x為2.5秒或3.1秒時,△EDQ為直角三角形
解析:略


 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:
 23、如圖,在△ABC中,CD⊥AB,垂足為D,點E在BC上,EF⊥AB,垂足為F.
23、如圖,在△ABC中,CD⊥AB,垂足為D,點E在BC上,EF⊥AB,垂足為F.查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 18、如圖,在△ABC中,邊AC的垂直平分線交BC于點D,交AC于點E、已知△ABC中與△ABD的周長分別為18cm和12cm,則線段AE的長等于
18、如圖,在△ABC中,邊AC的垂直平分線交BC于點D,交AC于點E、已知△ABC中與△ABD的周長分別為18cm和12cm,則線段AE的長等于查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com