
【題目】生物學上研究表明:不同濃度的生長素對植物的生長速度影響不同,在一定范圍內,生長素的濃度對植物的生長速度有促進作用,相反,在某些濃度范圍,生長速度會變緩慢,甚至阻礙植物生長(阻礙即植物不生長,甚至枯萎).小林同學在了解到這一信息后,決定研究生長素濃度與茶樹生長速度的關系,設生長素濃度為x克/升,生長速度為y毫米/天,當x超過4時,茶樹的生長速度y與生長素x濃度滿足關系式:![]() .實驗數據如下表,當生長速度為0時,實驗結束.
.實驗數據如下表,當生長速度為0時,實驗結束.
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 2 | 4 | 6 | 8 | 10 | 9 | 7 | 4 | 0 |
(1)如圖,建立平面直角坐標系xOy,描出表中各對對應值為坐標的點,畫出該函數圖象;
(2)根據上述表格,求出整個實驗過程中y與x的函數關系式,并寫出自變量x的取值范圍;
(3)結合畫出的函數圖象,寫出該函數的一條性質: ;
(4)若直線y=kx+3與上述函數圖象有2個交點,則k的取值范圍是: .
【答案】(1)畫出該函數圖象如圖所示;見解析;(2)
(3)當0<x<4時,y隨x的增大而增大;(4)![]() .
.
【解析】
(1)把表中的x,y的值分別描入平面直角坐標系中,再用直線或平滑的曲線連接即可;
(2)利用待定系數法進行求解,當0<x<4時,函數圖像是直線,當4≤x≤8時,函數圖像是拋物線;
(3)當0<x<4時,函數圖像是直線,![]() ,y隨x的增大而增大;
,y隨x的增大而增大;
(4)直線y=kx+3過點(0,3),要與上述函數圖像有2個交點,則直線過點(4,10)或(8,0),代入求解出k的值,進而求出k的取值范圍.
(1)畫出該函數圖象如圖所示;
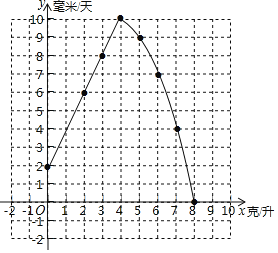
(2)當0<x<4時,設y=kx+b,
把(0,2),(2,6)代入y=kx+b得,![]() ,
,
解得:![]() ,
,
∴y=2x+2;
當4≤x≤8時,
把(7,4),(8,0)代入![]() 得,
得,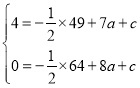
解得:![]()
∴y=﹣![]() x2+
x2+![]() x+4;
x+4;
∴整個實驗過程中y與x的函數關系式為: ;
;
(3)當0<x<4時,y隨x的增大而增大,
故答案為:當0<x<4時,y隨x的增大而增大;
(4)∵直線y=kx+3與上述函數圖象有2個交點,
∴當直線y=kx+3過(4,10)或(8,0)時,
即把(4,10)或(8,0)分別代入y=kx+3得,k=![]() 或k=﹣
或k=﹣![]() ,
,
∴若直線y=kx+3與上述函數圖象有2個交點,則k的取值范圍是:![]()
故答案為:![]() .
.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖是某路燈在鉛垂面內的示意圖,燈柱BC的高為10米,燈柱BC與燈桿AB的夾角為120°.路燈采用錐形燈罩,在地面上的照射區域DE的長為13.3米,從D、E兩處測得路燈A的仰角分別為α和45°,且tanα=6.求燈桿AB的長度.
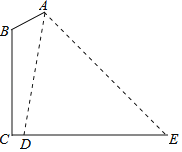
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在每個小正方形的邊長為![]() 的網格圖形中,每個小正方形的頂點稱為格點.從一個格點移動到與之相距
的網格圖形中,每個小正方形的頂點稱為格點.從一個格點移動到與之相距![]() 的另一個格點的運動稱為一次跳馬變換.例如,在
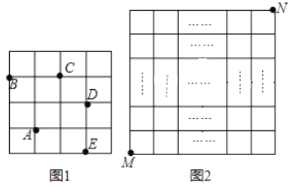
的另一個格點的運動稱為一次跳馬變換.例如,在![]() 的正方形網格圖形中(如圖1),從點
的正方形網格圖形中(如圖1),從點![]() 經過一次跳馬變換可以到達點
經過一次跳馬變換可以到達點![]() ,
,![]() ,
,![]() ,
,![]() 等處現有
等處現有![]() 的正方形網格圖形(如圖2),則從該正方形的頂點
的正方形網格圖形(如圖2),則從該正方形的頂點![]() 經過跳馬變換到達與其相對的頂點
經過跳馬變換到達與其相對的頂點![]() ,最少需要跳馬變換的次數是( )
,最少需要跳馬變換的次數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,AB=CD,點E、F在BC上,且BE=CF.
(1)求證:△ABE≌△DCF;
(2)試證明:以A、F、D、E為頂點的四邊形是平行四邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
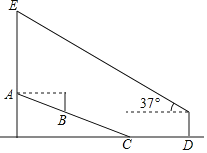
【題目】春天是放風箏的好時節,小明為了讓風箏順利起飛,特地將風箏放在坡度為1:2.4的山坡上,并站在視線剛好與風箏起飛點A齊平的B處,起風后小明開始往下跑26米至坡底C處,并繼續沿平地向前跑16米到達D處后站在原地開始調整,小明將手中的線軸剛好舉到與視線齊平處測得風箏的仰角是37°,此時風箏恰好升高到起飛時的正上方E處.已知小明視線距地面高度為1.5米,圖中風箏E、A、B、C、D五點在同一平面,則風箏上升的垂直距離AE約為( )米.(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.34.2B.32.7C.31.2D.22.7
查看答案和解析>>
科目:初中數學 來源: 題型:
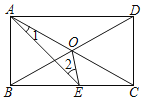
【題目】如圖,矩形ABCD中,對角線AC、BD交于點O,點E是BC上一點,且AB=BE,∠1=15°,則∠2的度數是( )
A.25°B.30°C.35°D.15°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=90°.
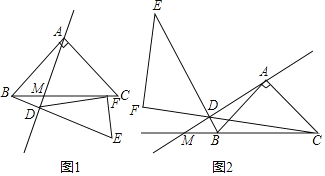
(1)如圖1,若直線AD與BC相交于M,過點B作AM的垂線,垂足為D,連接CD并延長BD至E,使得DE=DC,過點E作EF⊥CD于F,證明:AD=EF+BD.
(2)如圖2,若直線AD與CB的延長線相交于M,過點B作AM的垂線,垂足為D,連接CD并延長BD至E,使得DE=DC,過點E作EF⊥CD交CD的延長線于F,探究:AD、EF、BD之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題12分)如圖,AB是⊙O的直徑,BC為⊙O的切線,D為⊙O上的一點,CD=CB,延長CD交BA的延長線于點E.

(1)求證:CD為⊙O的切線;
(2)求證:∠C=2∠DBE.
(3)若EA=AO=2,求圖中陰影部分的面積.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
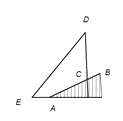
【題目】為踐行“綠水青山就是金山銀山”的重要思想,某森林保護區開展了尋找古樹活動.如圖,在一個坡度(或坡比)![]() =1:2.4的山坡AB上發現有一棵占樹CD.測得古樹底端C到山腳點A的距離AC=26米,在距山腳點A水平距離6米的點E處,測得古樹頂端D的仰角∠AED=48°(古樹CD與山坡AB的剖面、點E在同一平面上,古樹CD與直線AE垂直),則古樹CD的高度約為( )(參考數據:
=1:2.4的山坡AB上發現有一棵占樹CD.測得古樹底端C到山腳點A的距離AC=26米,在距山腳點A水平距離6米的點E處,測得古樹頂端D的仰角∠AED=48°(古樹CD與山坡AB的剖面、點E在同一平面上,古樹CD與直線AE垂直),則古樹CD的高度約為( )(參考數據:![]() °≈0.73,cos8°≈0.67,tan48°≈1.11)
°≈0.73,cos8°≈0.67,tan48°≈1.11)
A.17.0米B.21.9米C.23.3米D.33.3米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com