
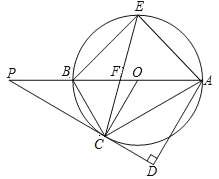
【題目】如圖所示,AB 是⊙O 的直徑,P 為 AB 延長線上的一點,PC 切⊙O 于點 C,AD⊥PC, 垂足為 D,弦 CE 平分∠ACB,交 AB 于點 F,連接 AE.
(1)求證:PC=PF;
(2)若 tan∠ABC=![]() ,AE=5
,AE=5![]() ,求線段 PC 的長.
,求線段 PC 的長.
【答案】(1)見解析;(2)PC=12.
【解析】(1)由切線得:OC⊥PC,再得平行,由同圓的半徑相等:OA=OC,根據等邊對等角可得結論;
(2)證明∠PFC=∠PCF,根據等角對等邊可得結論;
(3)根據三角函數的比設未知數,利用勾股定理列方程可得結論.
(1)證明:∵PC 為⊙O 的切線,
∴OC⊥PC,
∵AD⊥PC,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠DAC=∠OAC,
∴AC 平分∠DAB;
∵CE 平分∠ACB,
∴∠ACE=∠BCE,
∴![]() ,
,
∴∠ABE=∠ECB,
∵∠BCP+∠OCB=∠BCP+∠OBC=∠BAC+∠OBC=90°,
∴∠BCP=∠BAC,
∵∠BAC=∠BEC,
∴∠BCP=∠BEC,
∵∠PFC=∠BEC+∠ABE,∠PCF=∠ECB+∠BCP,
∴∠PFC=∠PCF,
∴PC=PF;
(2)∵![]() ,
,
∴AE=BE=5![]() ,
,
又∵AB 是直徑,
∴∠AEB=90°,
AB=![]() BE=10,
BE=10,
∴OB=OC=5,
∵∠PCB=∠PAC,∠P=∠P,
∴△PCB∽△PAC,
∴![]() ,
,
∵tan∠ABC=![]() ,
,
∴![]() .
.
設 PB=2x,則 PC=3x,
在 Rt△POC 中,(2x+5)2=(3x)2+52, 解得 x1=0(舍)x2=4,
∵x>0,
∴x=4,
∴PC=3x=3×4=12.


科目:初中數學 來源: 題型:
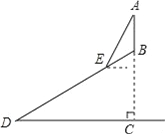
【題目】如圖,某班數學興趣小組利用數學活動課時間測量位于山頂的電視塔AB的高度,已知山的坡度為30°,山高857.5尺,組員從山腳D處沿山坡向著電視塔方向前進1620尺到達E點,在點E處測得電視塔頂端A的仰角為60°,求電視塔AB的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() 的邊
的邊![]() 上有一動點
上有一動點![]() ,從距離
,從距離![]() 點
點![]() 的點
的點![]() 處出發,沿線段
處出發,沿線段![]() 、射線
、射線![]() 運動,速度為
運動,速度為![]() ;動點
;動點![]() 從點
從點![]() 出發,沿射線
出發,沿射線![]() 運動,速度為
運動,速度為![]() ;
;![]() 、
、![]() 同時出發,同時射線
同時出發,同時射線![]() 繞著點
繞著點![]() 從
從![]() 上以每秒5°的速度順時針旋轉,設運動時間是
上以每秒5°的速度順時針旋轉,設運動時間是![]() .
.
(1)當點![]() 在
在![]() 上運動時,
上運動時,![]()
![]() (用含
(用含![]() 的代數式表示);
的代數式表示);
(2)當點![]() 在線段
在線段![]() 上運動時,
上運動時,![]() 為何值時,
為何值時,![]() ?此時射線
?此時射線![]() 是
是![]() 的角平分線嗎?如果是請說明理由.
的角平分線嗎?如果是請說明理由.
(3)在射線![]() 上是否存在
上是否存在![]() 、
、![]() 相距
相距![]() ?若存在,請求出t的值并求出此時
?若存在,請求出t的值并求出此時![]() 的度數;若不存在,請說明理由.
的度數;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】臺灣是中國領土不可分割的一部分,兩岸在政治、經濟、文化等領域交流越來越深,在北京故宮博物院成立90周年院慶時,兩岸故宮同根同源,合作舉辦了多項紀念活動.據統計,北京故宮博物院與臺北故宮博物院現共有藏品約245萬件,其中臺北故宮博物院藏品數量比北京故宮博物院藏品數量的![]() 還少25萬件,求北京故宮博物院約有多少萬件藏品?
還少25萬件,求北京故宮博物院約有多少萬件藏品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知線段![]() ,點
,點![]() 為線段
為線段![]() 上的一個動點,點
上的一個動點,點![]() 分別是
分別是![]() 和
和![]() 的中點.
的中點.
(1)若點![]() 恰好是
恰好是![]() 中點,則
中點,則![]()
![]() ;
;
(2)若![]() ,求
,求![]() 的長;
的長;
(3)試利用“字母代替數”的方法,說明不論![]() 取何值(不超過
取何值(不超過![]() ),
),![]() 的長不變.
的長不變.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 三點在數軸上所對應的數分別為
三點在數軸上所對應的數分別為![]() 且
且![]() 滿足
滿足![]() .動點
.動點![]() 從點
從點![]() 出發,以2單位/秒的速度向右運動,同時,動點
出發,以2單位/秒的速度向右運動,同時,動點![]() 從點
從點![]() 出發,以1單位秒的速度向左運動,線段
出發,以1單位秒的速度向左運動,線段![]() 為“變速區”,規則為: 從點
為“變速區”,規則為: 從點![]() 運動到點
運動到點![]() 期間速度變為原來的一半,之后立刻恢復原速,從點
期間速度變為原來的一半,之后立刻恢復原速,從點![]() 運動到點
運動到點![]() 期間速度變為原來的兩倍,之后也立刻恢復原速.當點
期間速度變為原來的兩倍,之后也立刻恢復原速.當點![]() 到達點
到達點![]() 時,兩點都停止運動.設運動的時間為
時,兩點都停止運動.設運動的時間為![]() 秒.
秒.
(1) ![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)①動點![]() 從點
從點![]() 運動至點
運動至點![]() 時,求
時,求![]() 的值;
的值;
②![]() 兩點相遇時,求相遇點在數軸上所對應的數;
兩點相遇時,求相遇點在數軸上所對應的數;
(3)若點![]() 為線段
為線段![]() 中點,當
中點,當![]() ________秒時,
________秒時,![]() .
.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
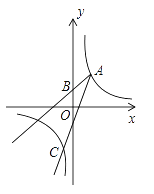
【題目】如圖,已知點A(2,3)和點B(0,2),點A在反比例函數y= ![]() 的圖象上.作射線AB,再將射線AB繞點A按逆時針方向旋轉45°,交反比例函數圖象于點C,則點C的坐標為________.
的圖象上.作射線AB,再將射線AB繞點A按逆時針方向旋轉45°,交反比例函數圖象于點C,則點C的坐標為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】寧波至紹興城際列車已于2019年7月10日運營,這是國內首條利用既有鐵路改造開行的跨市域城際鐵路.其中余姚至紹興的成人票價12元/人,學生票價6元/人.余姚某校801班師生共計50人坐城際列車去紹興秋游.
(1)設有![]() 名老師,求801班師生從余姚到紹興的城際列車總費用
名老師,求801班師生從余姚到紹興的城際列車總費用![]() 關于
關于![]() 的函數表達式.
的函數表達式.
(2)若從余姚到紹興的城際列車總費用![]() 不超過330元,問至少有幾名學生?
不超過330元,問至少有幾名學生?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知某個圖形是按下面方法連接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)請連接圖案,它是一個什么漢字?
(2)作出這個圖案關于y軸的軸對稱圖形,并寫出新圖案相應各端點的坐標,你得到一個什么漢字?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com