
【題目】在矩形ABCD中,AB=6cm,BC=12cm,點P從點A出發,沿AB邊向點B以每秒1cm的速度移動,同時,點Q從點B出發沿BC邊向點C以每秒2cm的速度移動.如果P、Q兩點在分別到達B、C兩點后就停止移動,回答下列問題:
(1)運動開始后第幾秒時,△PBQ的面積等于8cm2?
(2)當運動開始后![]() 秒時,試判斷△DPQ的形狀;
秒時,試判斷△DPQ的形狀;
(3)在運動過程中,是否存在這樣的時刻,使以Q為圓心,PQ為半徑的圓正好經過點D?若存在,求出運動時間;若不存在,請說明理由.
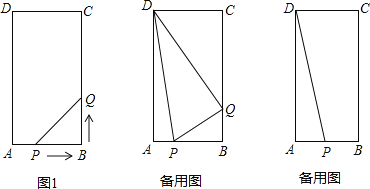
【答案】(1)t=2或4,即經過2秒或4秒,△PBQ的面積等于8cm2;
(2)△DPQ為直角三角形;
(3)運動開始后第6![]() ﹣18秒時,以Q為圓心,PQ為半徑的圓正好經過點D.
﹣18秒時,以Q為圓心,PQ為半徑的圓正好經過點D.
【解析】試題分析:(1)設出運動所求的時間,可將BP和BQ的長表示出來,代入三角形面積公式,列出等式,可將時間求出;(2)表示出DP2=![]() ,PQ2=
,PQ2=![]() ,DQ2=117,進而得到PQ2+DQ2=DP2,得出答案;(3)假設運動開始后第x秒時,滿足條件,則有QP=QD,表示出QP2,QD2,列出等式,整理得到方程,求出方程的解,根據時間大于0秒小于6秒,即可解答.
,DQ2=117,進而得到PQ2+DQ2=DP2,得出答案;(3)假設運動開始后第x秒時,滿足條件,則有QP=QD,表示出QP2,QD2,列出等式,整理得到方程,求出方程的解,根據時間大于0秒小于6秒,即可解答.
試題解析:(1)設經過t秒,△PBQ的面積等于8cm2,
則:BP=6﹣t,BQ=2t,
所以![]() ×(6﹣t)×2t=8,即t2﹣6t+8=0,
×(6﹣t)×2t=8,即t2﹣6t+8=0,
可得:t=2或4,即經過2秒或4秒,△PBQ的面積等于8cm2.
(2)當t=![]() 秒時,
秒時,
AP=![]() ,BP=6﹣
,BP=6﹣![]() =
=![]() ,BQ=
,BQ=![]() ×2=3,CQ=12﹣3=9,
×2=3,CQ=12﹣3=9,
∴在Rt△DAP中,![]() ,
,
在Rt△DCQ中,DQ2=DC2+CQ2=62+92=117,
在Rt△QBP中,![]() ,
,
∴![]() ,
,
∴DQ2+QP2=DP2,
∴△DPQ為直角三角形;
(3)假設運動開始后第x秒時,滿足條件,則:QP=QD,
∵OP2=PB2+BQ2=(6﹣x)2+(2x)2,
QD2=QC2+CD2=(12﹣2x)2+62,
∴(12﹣2x)2+62=(6﹣x)2+(2x)2,
整理,得:x2+36x﹣144=0,
解得:x=﹣18±6![]() ,
,
∵0<6![]() ﹣18<6,
﹣18<6,
∴運動開始后第6![]() ﹣18秒時,以Q為圓心,PQ為半徑的圓正好經過點D.
﹣18秒時,以Q為圓心,PQ為半徑的圓正好經過點D.


科目:初中數學 來源: 題型:
【題目】為減少環境污染,自2008年6月1日起,全國的商品零售場所開始實行“塑料購物袋有償使用制度”(以下簡稱“限塑令”).某班同學于6月上旬的一天,在某超市門口采用問卷調查的方式,隨機調查了“限塑令”實施前后,顧客在該超市用購物袋的情況,以下是根據100位顧客的100份有效答卷畫出的統計圖表的一部分:
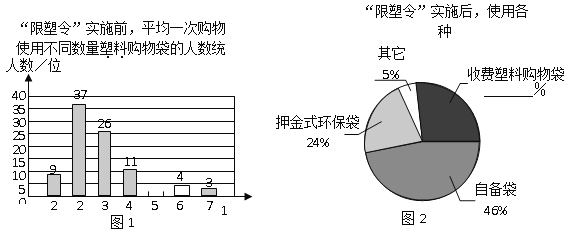
“限塑令”實施后,塑料購物袋使用后的處理方式統計表
處理方式 | 直接丟棄 | 直接做垃圾袋 | 再次購物使用 | 其它 |
選該項的人數占 總人數的百分比 | 5% | 35% | 49% | 11% |
請你根據以上信息解答下列問題:
(1)補全圖1,“限塑令”實施前,如果每天約有2 000人次到該超市購物.根據這100位顧客平均一次購物使用塑料購物袋的平均數,估計這個超市每天需要為顧客提供多少個塑料購物袋?
(2)補全圖2,并根據統計圖和統計表說明,購物時怎樣選用購物袋,塑料購物袋使用后怎樣處理,能對環境保護帶來積極的影響.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,對角線AC與BD相交于點O,AF平分∠BAC,交BD于點F.
(1)求證: ![]() ;
;
(2)點A1、點C1分別同時從A、C兩點出發,以相同的速度運動相同的時間后同時停止,如圖,A1F1平分∠BA1C1 , 交BD于點F1 , 過點F1作F1E⊥A1C1 , 垂足為E,請猜想EF1 , AB與 ![]() 三者之間的數量關系,并證明你的猜想;
三者之間的數量關系,并證明你的猜想;
(3)在(2)的條件下,當A1E1=6,C1E1=4時,求BD的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】不透明的布袋里裝有紅、藍、黃三種顏色小球共40個,它們除顏色外其余都相同,其中紅色球20個,藍色球比黃色球多8個.
(1)求袋中藍色球的個數;
(2)現再將2個黃色球放入布袋,攪勻后,求摸出1個球是黃色球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
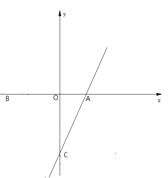
【題目】如圖,二次函數![]() 的圖像交
的圖像交![]() 軸于
軸于![]() ,交
,交![]() 軸于點
軸于點![]() ,連接直線
,連接直線![]() .
.
(1)求二次函數的解析式;
(2)點![]() 在二次函數的圖像上,圓
在二次函數的圖像上,圓![]() 與直線
與直線![]() 相切,切點為
相切,切點為![]() .
.
①若![]() 在
在![]() 軸的左側,且△
軸的左側,且△![]() ∽△
∽△![]() ,求點
,求點![]() 的坐標;
的坐標;
②若圓![]() 的半徑為4,求點
的半徑為4,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題是真命題的是( )
A.如果兩個角不相等,那么這兩個角不是對頂角;B.兩互補的角一定是鄰補角.
C.如果a2=b2,那么a=b;D.如果兩角是同位角,那么這兩角一定相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校舉辦八年級學生數學素養大賽,比賽共設四個項目:七巧板拼圖,趣題巧解,數學應用,魔方復原,每個項目得分都按一定百分比折算后記入總分,下表為甲,乙,丙三位同學得分情況(單位:分)
七巧板拼圖 | 趣題巧解 | 數學應用 | 魔方復原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比賽后,甲猜測七巧板拼圖,趣題巧解,數學應用,魔方復原這四個項目得分分別按10%,40%,20%,30%折算△記入總分,根據猜測,求出甲的總分;
(2)本次大賽組委會最后決定,總分為80分以上(包含80分)的學生獲一等獎,現獲悉乙,丙的總分分別是70分,80分.甲的七巧板拼圖、魔方復原兩項得分折算后的分數和是20分,問甲能否獲得這次比賽的一等獎?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com