
【題目】如圖,在正方形ABCD中,對角線AC與BD相交于點O,AF平分∠BAC,交BD于點F.
(1)求證: ![]() ;
;
(2)點A1、點C1分別同時從A、C兩點出發,以相同的速度運動相同的時間后同時停止,如圖,A1F1平分∠BA1C1 , 交BD于點F1 , 過點F1作F1E⊥A1C1 , 垂足為E,請猜想EF1 , AB與 ![]() 三者之間的數量關系,并證明你的猜想;
三者之間的數量關系,并證明你的猜想;
(3)在(2)的條件下,當A1E1=6,C1E1=4時,求BD的長
【答案】
(1)解:過F作FG⊥AB于G,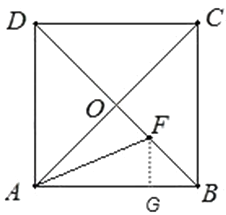
∵AF平分∠CAB,FO⊥AC,FG⊥AB,
∴OF=FG,
∵∠AOF=∠AGF=90°,AF=AF,OF=FG,
∴△AOF≌△AGF,
∴AO=AG,
直角三角形BGF中,∠DGA=45°,
∴FG=BG=OF,
∴AB=AG+BG=AO+OF= ![]() AC+OF,
AC+OF,
∴AB-OF= ![]() AC
AC
(2)解:過F1作F1G1⊥A1B,過F1作F1H1⊥BC1 , 
則四邊形F1G1BH1是矩形.
同(1)可得EF1=F1G,因此四邊形F1G1BH1是正方形.
∴EF1=G1F1=F1H1 ,
即:F1是三角形A1BC1的內心,
∴EF1=(A1B+BC1-A1C1)÷2…①
∵A1B+BC1=AB+A1A+BC-CC1 , 而CC1=A1A,
∴A1B+BC1=2AB,
因此①式可寫成:EF1=(2AB-A1C1)÷2,
即AB-EF1= ![]() A1C1
A1C1
(3)解:由(2)得,F1是三角形A1BC1的內心,且E1、G1、H1都是切點.
∴A1E=(A1C1+A1B-BC1)÷2,
如果設CC1=A1A=x,
A1E=[A1C1+(AB+x)-(AB-x)]÷2=(10+2x)÷2=6,
∴x=1,
在直角三角形A1BC1中,根據勾股定理有A1B2+BC12=AC12 ,
即:(AB+1)2+(AB-1)2=100,
解得AB=7,
∴BD=7 ![]() .
.
【解析】(1)過F作FG⊥AB于G,根據已知條件可證△AOF≌△AGF,結合直角三角形的性質可求解;(2)過F1作F1G1⊥A1B,過F1作F1H1⊥BC1 , 根據已知條件可得四邊形F1G1BH1是矩形,再證四邊形F1G1BH1是正方形,則結論可證;(3)在直角三角形A1BC1中,根據勾股定理可求解。


科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AC=BD,M,N分別是AB,CD的中點,MN分別交BD和AC于點E,F,對角線AC和BD相交于點G,則GE和GF相等嗎?為什么?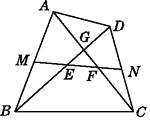
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】太原市第 37 中學校 A 同學在新冠疫情期間,媽媽每天為其測量體溫,為了較直觀地了 解這位同學這個月的日期和每天體溫的變化趨勢,可選擇的比較好的方法是( )
A.表格法B.圖象法C.關系式法D.以上三種方法均可
查看答案和解析>>
科目:初中數學 來源: 題型:
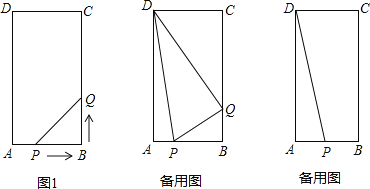
【題目】在矩形ABCD中,AB=6cm,BC=12cm,點P從點A出發,沿AB邊向點B以每秒1cm的速度移動,同時,點Q從點B出發沿BC邊向點C以每秒2cm的速度移動.如果P、Q兩點在分別到達B、C兩點后就停止移動,回答下列問題:
(1)運動開始后第幾秒時,△PBQ的面積等于8cm2?
(2)當運動開始后![]() 秒時,試判斷△DPQ的形狀;
秒時,試判斷△DPQ的形狀;
(3)在運動過程中,是否存在這樣的時刻,使以Q為圓心,PQ為半徑的圓正好經過點D?若存在,求出運動時間;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥DE,AC∥DF,AC=DF,下列條件中,不能判斷△ABC≌△DEF的是( )
A.AB=DE
B.∠B=∠E
C.EF=BC
D.EF∥BC
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com