
【題目】如圖,某路燈在鉛垂面內的示意圖,燈柱AB的高為13米,燈桿BC與燈柱AB的夾角∠B=120°,路燈采用錐形燈罩,在地面上的照射區域DE長為20米,已知tan∠CDE=![]() ,tan∠CED=
,tan∠CED=![]() ,求燈桿BC的長度.
,求燈桿BC的長度.
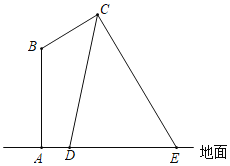
【答案】燈桿CB的長度為2米
【解析】
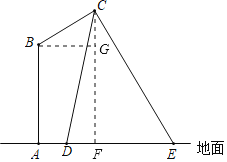
過點C作CF⊥AE,交AE于點F,過點B作BG⊥CF,交CF于點G,設CF=7x,則EF=8x,根據銳角三角函數的性質求出x的值,即CG=1,再根據含30°角的直角三角形的性質求出BC的長度即可.
解:過點C作CF⊥AE,交AE于點F,過點B作BG⊥CF,交CF于點G,則FG=BA=13.
∵tan∠CDE=![]() ,tan∠CED=
,tan∠CED=![]() ,
,
設CF=7x,則EF=8x.
在Rt△CDF中,
∵tan∠CDF=![]() ,
,
∴DF=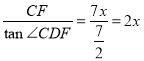 ,
,
∵DE=20,
∴2x+8x=20.
∴x=2.
∴CG=CF﹣GF=14﹣13=1.
∵∠ABC=120°,
∴∠CBG=∠ABC﹣∠ABG=120°﹣90°=30°.
∴CB=2CG=2,
答:燈桿CB的長度為2米.


科目:初中數學 來源: 題型:
【題目】如圖,若點M是![]() 軸正半軸上任意一點,過點M作PQ∥
軸正半軸上任意一點,過點M作PQ∥![]() 軸,分別交函數
軸,分別交函數![]() 和
和![]() 的圖象于點P和Q,連接OP和OQ.則下列結論正確的是( )
的圖象于點P和Q,連接OP和OQ.則下列結論正確的是( )

A.∠POQ不可能等于90°B.![]()
C.這兩個函數的圖象一定關于![]() 軸對稱D.△POQ的面積是
軸對稱D.△POQ的面積是![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
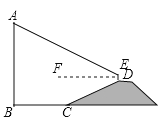
【題目】如圖,![]() 是垂直于水平面的建筑物,為測量
是垂直于水平面的建筑物,為測量![]() 的高度,小紅從建筑物底端
的高度,小紅從建筑物底端![]() 出發,沿水平方向行走了52米到達點
出發,沿水平方向行走了52米到達點![]() ,然后沿斜坡
,然后沿斜坡![]() 前進,到達坡頂
前進,到達坡頂![]() 點處,
點處,![]() .在點
.在點![]() 處放置測角儀,測角儀支架
處放置測角儀,測角儀支架![]() 高度為0.8米,在
高度為0.8米,在![]() 點處測得建筑物頂端
點處測得建筑物頂端![]() 點的仰角
點的仰角![]() 為
為![]() (點
(點![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面內),斜坡
在同一平面內),斜坡![]() 的坡度(或坡比)
的坡度(或坡比)![]() ,求建筑物
,求建筑物![]() 的高度.(精確到個位)(參考數據:
的高度.(精確到個位)(參考數據:![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
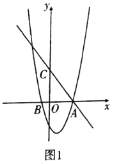
【題目】已知:如圖1,拋物線![]() 是由拋物線
是由拋物線![]() 向右平移1個單位,再向下平移4個單位得到的,
向右平移1個單位,再向下平移4個單位得到的,![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點(
兩點(![]() 在
在![]() 的右側),直線
的右側),直線![]() 經過點
經過點![]() ,與
,與![]() 軸交于
軸交于![]() 點.
點.
(1)分別求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)如圖2,已知![]() 點是線段
點是線段![]() 上任一點(不與
上任一點(不與![]() ,
,![]() 重合),過
重合),過![]() 點作
點作![]() 軸垂線,交拋物線
軸垂線,交拋物線![]() 于
于![]() 點.當
點.當![]() 在何處時,四邊形
在何處時,四邊形![]() 面積最大,求出此時
面積最大,求出此時![]() 點坐標及四邊形
點坐標及四邊形![]() 面積的最大值.
面積的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題探究,
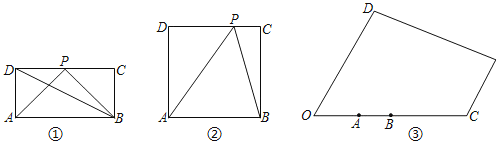
(1)如圖①,在矩形ABCD中,AB=2AD,P為CD邊上的中點,試比較∠APB和∠ADB的大小關系,并說明理由;
(2)如圖②,在正方形ABCD中,P為CD上任意一點,試問當P點位于何處時∠APB最大?并說明理由;
問題解決
(3)某兒童游樂場的平面圖如圖③所示,場所工作人員想在OD邊上點P處安裝監控裝置,用來監控OC邊上的AB段,為了讓監控效果最佳,必須要求∠APB最大,已知:∠DOC=60°,OA=400米,AB=200![]() 米,問在OD邊上是否存在一點P,使得∠APB最大,若存在,請求出此時OP的長和∠APB的度數;若不存在,請說明理由.
米,問在OD邊上是否存在一點P,使得∠APB最大,若存在,請求出此時OP的長和∠APB的度數;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
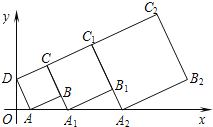
【題目】在平面坐標系中,第1個正方形ABCD的位置如圖所示,點A的坐標為(3,0),點D的坐標為(0,4),延長CB交x軸于點A1,作第2個正方形A1B1C1C,延長C1B1交x軸于點A2;作第3個正方形A2B2C2C1,…按這樣的規律進行下去,第5個正方形的邊長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
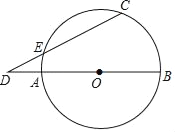
【題目】如圖,AB是⊙O的直徑,點C是⊙O上一點,點D在BA的延長線上,CD與⊙O交于另一點E,DE=OB=2,∠D=20°,則弧BC的長度為( )
A. ![]() π B.
π B. ![]() π C.
π C. ![]() π D.
π D. ![]() π
π
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著人們的生活水平的提高,家用轎車越來越多地進入家庭.小明家買了一輛小轎車,他連續記錄了7天中每天行駛的路程(如下表),以50km為標準,多于50km的記為“+”,不足50km的記為“﹣”,剛好50km的記為“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣9 | ﹣13 | 0 | ﹣14 | ﹣16 | +33 | +19 |
(1)求出這7天的行駛路程中最多的一天比最少的一天多行駛多少千米?
(2)若每行駛100km需用汽油8升,每升汽油6.5元,計算小明家這7天的汽油費用共是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應黨的“文化自信”號召,某校開展了古詩詞誦讀大賽活動,現隨機抽取部分同學的成績進行統計,并繪制成如下的兩個不完整的統計圖,請結合圖中提供的信息,解答下列各題:
(1)直接寫出a的值,a= ,并把頻數分布直方圖補充完整.
(2)求扇形B的圓心角度數.
(3)如果全校有2000名學生參加這次活動,90分以上(含90分)為優秀,那么估計獲得優秀獎的學生有多少人?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com