
【題目】已知四邊形 ABCD ,有以下四個條件:① AB ∥ CD ;② BC ∥ AD ;③ AB CD ;④ABC ADC .從這四個條件中任選兩個,能使四邊形 ABCD 成為平行四邊形的選法有( )
A.3 種B.4 種C.5 種D.6 種
【答案】B
【解析】
從四個條件中任選兩個,共有以下6種組合:①②、①③、①④、②③、②④、③④,然后按照平行四邊形的判定方法逐一判斷即可.
解:從四個條件中任選兩個,共有以下6種組合:①②、①③、①④、②③、②④、③④;
具備①②時,四邊形ABCD滿足兩組對邊分別平行,是平行四邊形;
具備①③時,四邊形ABCD滿足一組對邊平行且相等,是平行四邊形;
具備①④時,如圖,∵AB ∥ CD ,∴ABC +C=180°.
∵ABC ADC,∴ADC +C=180°.
∴AD∥CB .
所以四邊形 ABCD 是平行四邊形;
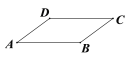
具備②③時,等腰梯形就符合一組對邊平行,另一組對邊相等,但它不是平行四邊形,故具備②③時,不能判斷是否是平行四邊形;
具備②④時,類似于上述①④,可以證明四邊形 ABCD 是平行四邊形;
具備③④時,如圖,四邊形ABCD為平行四邊形,連接AC,作AE垂直BC于E;
在EB上截取EC'=EC,連接AC',則△AEC'≌△AEC,AC'=AC.
把△ACD繞點A順時針旋轉∠CAC'的度數,則AC與AC'重合.
顯然四邊形ABC'D' 滿足:AB=CD=C'D';∠B=∠D=∠D',而四邊形ABC'D'并不是平行四邊形.
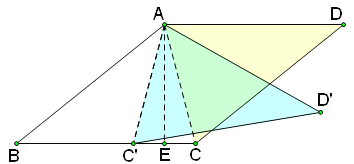
綜上,從四個條件中任選兩個,能使四邊形 ABCD 成為平行四邊形的選法共有4種.
故選B.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知一副三角板按如圖1方式拼接在一起,其中邊OA、OC與直線EF重合,![]() ,
,![]()
![]() 圖1中
圖1中![]() ______
______![]()
![]() 如圖2,三角板COD固定不動,將三角板AOB繞著點O按順時針方向旋轉一個角度
如圖2,三角板COD固定不動,將三角板AOB繞著點O按順時針方向旋轉一個角度![]() ,在轉動過程中兩塊三角板都在直線EF的上方:
,在轉動過程中兩塊三角板都在直線EF的上方:
![]() 當OB平分OA、OC、OD其中的兩邊組成的角時,求滿足要求的所有旋轉角度
當OB平分OA、OC、OD其中的兩邊組成的角時,求滿足要求的所有旋轉角度![]() 的值;
的值;
![]() 是否存在
是否存在![]() ?若存在,求此時的
?若存在,求此時的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上有A、B兩點(點A在點B的左側),且兩點距離為8個單位長度,動點P從點A出發,以每秒2個單位長度的速度沿數軸向右勻速運動,設運動時間為t(t>0)秒.
![]()
(1)圖中如果點A、B表示的數是互為相反數,那么點A表示的數是 ;
(2)當t=3秒時,點A與點P之間的距離是 個長度單位;
(3)當點A表示的數是-3時,用含t的代數式表示點P表示的數;
(4)若點P到點A的距離是點P到點B的距離的2倍,請直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
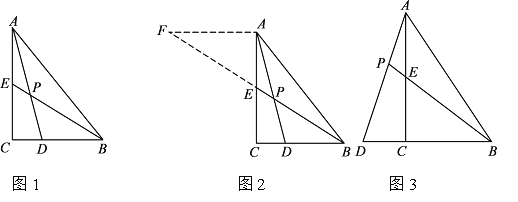
小昊遇到這樣一個問題:如圖1,在△ABC中,∠ACB=90°,BE是AC邊上的中線,點D在BC邊上,CD:BD=1:2,AD與BE相交于點P,求![]() 的值.
的值.
小昊發現,過點A作AF∥BC,交BE的延長線于點F,通過構造△AEF,經過推理和計算能夠使問題得到解決(如圖2).請回答:![]() 的值為 .
的值為 .
參考小昊思考問題的方法,解決問題:
如圖 3,在△ABC中,∠ACB=90°,點D在BC的延長線上,AD與AC邊上的中線BE的延長線交于點P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,則BP=__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,二次函數y=﹣![]() x2+bx+c的圖線與坐標軸分別交于點A、B、C,其中點A(0,8),OB=
x2+bx+c的圖線與坐標軸分別交于點A、B、C,其中點A(0,8),OB=![]() OA.
OA.
(1)求二次函數的表達式;
(2)若OD=OB,點F為該二次函數在第二象限內圖象上的動點,E為DF的中點,當△CEF的面積最大時,求出點E的坐標;
(3)將三角形CEF繞E旋轉180°,C點落在M處,若M恰好在該拋物線上,求出此時△CEF的面積.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從有關方面獲悉,在我市農村已經實行了農民新型合作醫療保險制度.享受醫保的農民可在規定的醫院就醫并按規定標準報銷部分醫療費用.下表是醫療費用報銷的標準:
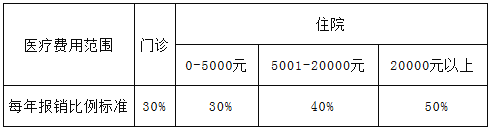
(說明:住院醫療費用為整數,住院醫療費用的報銷分段計算.如:某人住院醫療費用共30000元,則5000元按30%報銷、15000元按40%報銷、余下的10000元按50%報銷;題中涉及到的醫療費均指允許報銷的醫療費)
(1)甲農民一年內實際門診醫療費為2000元,則標準報銷的金額為 元;
乙農民一年住院醫療費為15000元,則按標準報銷的金額為 元;
(2)設某農民一年中住院的實際醫療費用為x元(5001≤x≤20000),按標準報銷的金額為多少元?(用含x的代數式表示)
(3)若某農民一年內本人自負住院醫療費17000元(自負醫療費=實際醫療費﹣按標準報銷的金額),則該農民當年實際醫療費用共多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學數學興趣小組為了解本校學生對電視節目的喜愛情況,隨機調查了部分學生最喜愛哪一類節目 (被調查的學生只選一類并且沒有不選擇的),并將調查結果制成了如下的兩個統計圖(不完整).請你根據圖中所提供的信息,完成下列問題:
(1)求本次調查的學生人數;
(2)請將兩個統計圖補充完整,并求出新聞節目在扇形統計圖中所占圓心角的度數;
(3)若該中學有2000名學生,請估計該校喜愛電視劇節目的人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個問題解決往往經歷發現猜想——探索歸納——問題解決的過程,下面結合一道幾何題來體驗一下.
(發現猜想)(1)如圖①,已知∠AOB=70°,∠AOD=100°,OC為∠BOD的角平分線,則∠AOC的度數為 ;.


(探索歸納)(2)如圖①,∠AOB=m,∠AOD=n,OC為∠BOD的角平分線. 猜想∠AOC的度數(用含m、n的代數式表示),并說明理由.
(問題解決)(3)如圖②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射線OB繞點O以每秒20°逆時針旋轉,射線OC繞點O以每秒10°順時針旋轉,射線OD繞點O每秒30°順時針旋轉,三條射線同時旋轉,當一條射線與直線OA重合時,三條射線同時停止運動. 運動幾秒時,其中一條射線是另外兩條射線夾角的角平分線?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖.在Rt△ABC中,∠A=90°,AB=AC=4.點E為Rt△ABC邊上一點,以每秒1單位的速度從點C出發,沿著C→A→B的路徑運動到點B為止.連接CE,以點C為圓心,CE長為半徑作⊙C,⊙C與線段BC交于點D.設扇形DCE面積為S,點E的運動時間為t.則在以下四個函數圖象中,最符合扇形面積S關于運動時間t的變化趨勢的是( )

A. 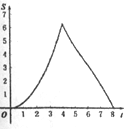 B.
B. 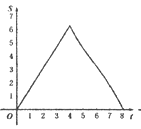
C. 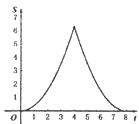 D.
D. 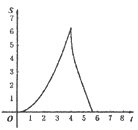
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com