
【題目】神奇的數學世界是不是只有鍛煉思維的數字游戲?每天都在面對繁雜的數字計算?答案當然是否定的,曼妙的數學暢游在迷人的數字和豐富多彩的圖形之間,將數與形巧妙地融匯在一起,不可分割.我們都知道,實數與數軸上的點一一對應,數軸上的線段可以由端點所對應的實數確定,這是一維的數與形;增加到兩條數軸,可以形成平面直角坐標系,這樣有序數對與平面內的點一一對應,平面內的多邊形及其內容可以由多邊形的邊上所有點的坐標所確定,這是二維的數與形.而在平面直角坐標系中的圖形更是神秘,在平面內任意畫一條(或多條)曲線(或直線),它(們)把平面分割成的部分都稱為區域,特別地,如果曲線首尾相接,那么形成的有限部分也稱為封閉區域.如何研究這些區域呢?當然離不開數,我們可以通過區域內點的坐標規律來刻畫圖形.反過來,我們也可以根據點坐標的規律在平面直角坐標系內找到它們,畫出相應的圖形.聰明的你看懂了嗎?試著做做看.
(1)分別解不等式![]() 和
和![]() ,并把不等式的解集畫在同一個數軸上;
,并把不等式的解集畫在同一個數軸上;
(2)點P(x,y)在平面直角坐標系的第一象限,并且橫坐標與縱坐標分別滿足不等式![]() 和
和![]() ,請畫出滿足條件的點P所在的最大區域,并求出區域的面積;
,請畫出滿足條件的點P所在的最大區域,并求出區域的面積;
(3)去掉(2)中“點P在第一象限”這個條件,其余條件保持不變,求滿足條件的點P所在最大區域與平面直角坐標系第二、四象限角平分線所圍成封閉區域的面積.
科目:初中數學 來源: 題型:
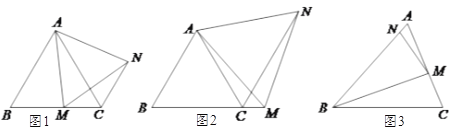
【題目】(Ⅰ)如圖1,在等邊![]() 中,點
中,點![]() 是
是![]() 上的任意一點(不含端點
上的任意一點(不含端點![]() ,
, ![]() ),連結
),連結![]() ,以
,以![]() 為邊作等邊
為邊作等邊![]() ,并連結
,并連結![]() .求證:
.求證: ![]() .
.
(Ⅱ)【類比探究】
如圖2,在等邊![]() 中,若點
中,若點![]() 是
是![]() 延長線上的任意一點(不含端點
延長線上的任意一點(不含端點![]() ),其它條件不變,則
),其它條件不變,則![]() 是否還成立?若成立,請說明理由;若不成立,請寫出
是否還成立?若成立,請說明理由;若不成立,請寫出![]() ,
, ![]() ,
, ![]() 三者間的數量關系,并給予證明.
三者間的數量關系,并給予證明.
(Ⅲ)【拓展延伸】
如圖3,在等腰![]() 中,
中, ![]() ,點
,點![]() 是
是![]() 上的任意一點(不含端點),連結
上的任意一點(不含端點),連結![]() ,以
,以![]() 為邊作等腰
為邊作等腰![]() ,使
,使![]() ,試探究
,試探究![]() 與
與![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,四邊形ABCD是正方形,點E是AB邊的中點,以AE為邊作正方形AEFG,連接DE,BG.
(1)發現
①線段DE、BG之間的數量關系是;
②直線DE、BG之間的位置關系是 .
(2)探究
如圖2,將正方形AEFG繞點A逆時針旋轉,(1)中的結論是否仍然成立?若成立,請給出證明;若不成立,請說明理由.
(3)應用
如圖3,將正方形AEFG繞點A逆時針旋轉一周,記直線DE與BG的交點為P,若AB=4,請直接寫出點P到CD所在直線距離的最大值和最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古希臘數學家把數1,3,6,10,15,21,…叫做三角形數,它有一定的規律性,若把第一個三角形數記為x1 , 第二個三角形數記為x2 , …第n個三角形數記為xn , 則xn+xn+1= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年《政府工作報告》中提出了十大新詞匯,為了解同學們對新詞匯的關注度,某數學興趣小組選取其中的A:“互聯網+政務服務”,B:“工匠精神”,C:“光網城市”,D:“大眾旅游時代”四個熱詞在全校學生中進行了抽樣調查,要求被調查的每位同學只能從中選擇一個我最關注的熱詞.根據調查結果,該小組繪制了如下的兩幅不完整的統計圖. 
請你根據統計圖提供的信息,解答下列問題:
(1)本次調查中,一共調查了多少名同學?
(2)條形統計圖中,m= , n=;
(3)扇形統計圖中,熱詞B所在扇形的圓心角是多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
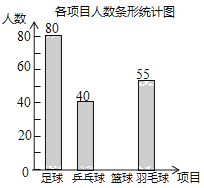
【題目】某學校準備開展“陽光體育活動”,決定開設以下體育活動項目:足球、乒乓球、籃球和羽毛球,要求每位學生必須且只能選擇一項,為了解選擇各種體育活動項目的學生人數,隨機抽取了部分學生進行調查,并將通過獲得的數據進行整理,繪制出以下兩幅不完整的統計圖,請根據統計圖回答問題:
(1)這次活動一共調查了 名學生;
(2)補全條形統計圖;
(3)在扇形統計圖中,選擇籃球項目的人數所在扇形的圓心角等于 度;
(4)若該學校有1500人,請你估計該學校選擇足球項目的學生人數約是 人。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,∠ABK的角平分線BE的反向延長線和∠DCK的角平分線CF的反向延長線交于點H,∠K﹣∠H=27°,則∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一只甲蟲在5×5的方格(每小格邊長為1)上沿著網格線運動.它從A處出發去看望B、C、D處的其它甲蟲,規定:向上向右走為正,向下向左走為負.如果從A到B記為:A→B(+1,+4),從B到A記為:B→A(-1,-4),其中第一個數表示左右方向,第二個數表示上下方向.
(1)圖中A→C( , ),B→C( , ),C→ (+1, );
(2)若這只甲蟲從A處去甲蟲P處的行走路線依次為(+2,+2),(+2,-1),(-2,+3),(-1,-2),請在圖中標出P的位置;

(3)若這只甲蟲的行走路線為A→B→C→D,請計算該甲蟲走過的路程;
(4)若圖中另有兩個格點M、N,且M→A(3-a,b-4),M→N(5-a,b-2),則N→A應記為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com