Question

1．將△ABC沿BC方向平移到△A′B′C′，且BB′=n•BC，連AC′交A′B′于D，交A′B′于E．

（1）如圖1，當n=2時，$\frac{DE}{AD}$=$\frac{2}{3}$，$\frac{EC'}{DE}$=$\frac{5}{4}$；
（2）如圖2，當E為DC′的中點時，求證：n=$\sqrt{2}$+1；
（3）當n=$\frac{1+\sqrt{3}}{2}$或2+$\sqrt{6}$時，點E是C′D的三等分點．

Answer 1

分析 （1）根據已知條件可知BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，得$\frac{A′E}{AB}=\frac{ED}{AD}=\frac{2}{3}$，$\frac{CE}{CA}=\frac{1}{3}$即可解答．
（2）根據$\frac{AD}{DC}=\frac{AA′}{BC′}$得$\frac{n-1}{2}=\frac{n}{n+1}$，解方程即可．
（3）分EC′=2DE或DE=2EC′兩種情形，通過比例式列出方程即可求出n．

解答 解：（1）如圖1中，連接AA′，
∵△A′B′C′是由△ABC平移，
∴BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，
∵BB′=2BC=2B′C′，
∴$\frac{B′E}{AB}$=$\frac{C′B′}{C′B}$=$\frac{1}{3}$，$\frac{CE}{AE}=\frac{C′B′}{B′B}$=$\frac{1}{2}$，
∴$\frac{A′E}{AB}=\frac{DE}{AD}$=$\frac{2}{3}$，$\frac{EC′}{DE}$=$\frac{5}{4}$，
故答案分別為$\frac{2}{3}$，$\frac{5}{4}$．
（2）∵△A′B′C′是由△ABC平移，
∴BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，BB′=nBC，
∴$\frac{EC}{AE}=\frac{C′B′}{BB′}$=$\frac{1}{n}$，
∵DE=EC，
∴$\frac{AD}{DC}=\frac{AA′}{BC′}$，
∴$\frac{n-1}{2}=\frac{n}{n+1}$，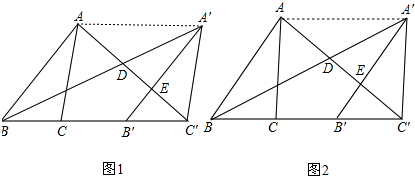
∴n²-2n-1=0
∴n=1+$\sqrt{2}$或1-$\sqrt{2}$
∵n＞0
∴n=1+$\sqrt{2}$．
（3）①當EC′=2DE時，
∵△A′B′C′是由△ABC平移，
∴BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，
∴$\frac{EC′}{AE}=\frac{B′C′}{B′B}$=$\frac{1}{n}$，
∴$\frac{AD}{DC}$=$\frac{AA′}{BC′}$，
∴$\frac{n-\frac{1}{2}}{\frac{1}{2}+1}=\frac{n}{n+1}$，
整理得到2n²-2n-1=0
∴n=$\frac{1+\sqrt{3}}{2}$或$\frac{1-\sqrt{3}}{2}$（舍棄）．
②當DE=2EC′時，
∵△A′B′C′是由△ABC平移，
∴BC=B′C′，AA′=BB′，AB=A′B′，AA′∥BB′，AB∥A′B′，
∴$\frac{EC′}{AE}=\frac{B′C′}{B′B}$=$\frac{1}{n}$，
∴$\frac{AD}{DC}$=$\frac{AA′}{BC′}$，
∴$\frac{n-2}{2+1}=\frac{n}{n+1}$，
整理得到：n²-4n-2=0
∴n=2+$\sqrt{6}$或2-$\sqrt{6}$（舍棄）．
故答案為$\frac{1+\sqrt{3}}{2}$或2+$\sqrt{6}$．

點評 本題考查平移的性質、平行成比例等知識，圖形比較復雜，靈活運用平行成比例是解決問題的關鍵，學會用方程的思想去解決問題．