
【題目】某校為了解九年級學生的身高情況,隨機抽取了部分學生的身高進行調查,利用所得數據繪成如下不完整的統計表和頻數分布直方圖,根據提供的信息解答下列問題:
身高分組( | 頻數 | 百分比 |
| 5 |
|
|
| |
| 15 |
|
| 14 |
|
| 6 |
|
總計 |
|
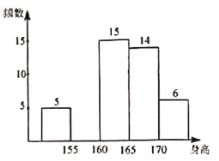
(1)![]() ______.
______.
(2)樣本中位數所在組別為______.
(3)通過計算補全頻數分布直方圖;
(4)該校九年級共有300名學生,估計身高不低于![]() 的學生有多少人.
的學生有多少人.
科目:初中數學 來源: 題型:
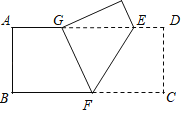
【題目】如圖,在長方形紙片ABCD中,AB=3,AD=9,折疊紙片ABCD,使頂點C落在邊AD上的點G處,折痕分別交邊AD、BC于點E、F,則△GEF的面積最大值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)定義:把四邊形的某些邊向兩方延長,其他各邊有不在延長所得直線的同一旁,這樣的四邊形叫做凹四邊形.如圖1,四邊形![]() 為凹四邊形.
為凹四邊形.
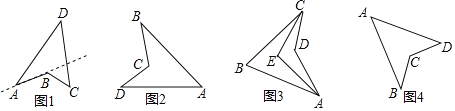
(2)性質探究:請完成凹四邊形一個性質的證明.
已知:如圖2,四邊形![]() 是凹四邊形.
是凹四邊形.
求證:![]() .
.
(3)性質應用:
如圖3,在凹四邊形![]() 中,
中,![]() 的角平分線與
的角平分線與![]() 的角平分線交于點
的角平分線交于點![]() ,若
,若![]() ,
,![]() ,則
,則![]() °.
°.
(4)類比學習:
如圖4,在凹四邊形![]() 中,點
中,點![]() 分別是邊
分別是邊![]() 的中點,順次連接各邊中點得到四邊形
的中點,順次連接各邊中點得到四邊形![]() .若
.若![]() ,則四邊形
,則四邊形![]() 是 .(填寫序號即可)
是 .(填寫序號即可)
A.梯形 B.菱形 C.矩形 D.正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() 為線段
為線段![]() 上一點,
上一點,![]() 為射線
為射線![]() 上一點,且
上一點,且![]() ,連接
,連接![]() .
.
(1)如圖1,若![]() ,請補全圖形并求
,請補全圖形并求![]() 的長;
的長;
(2)如圖2,若![]() ,連接
,連接![]() 并延長,交
并延長,交![]() 于點
于點![]() ,小明通過觀察、實驗提出猜想:
,小明通過觀察、實驗提出猜想:![]() .小明把這個猜想與同學們進行交流,通過討論,形成了證明該猜想的幾種想法:
.小明把這個猜想與同學們進行交流,通過討論,形成了證明該猜想的幾種想法:
想法1:過![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,先證出
,先證出![]() ,再證出
,再證出![]() 是等腰三角形即可;
是等腰三角形即可;
想法2:過![]() 作
作![]() 交
交![]() 于點
于點![]() ,先證出
,先證出![]() ,再證點
,再證點![]() 為線段
為線段![]() 的中點即可.
的中點即可.
請你參考上面的想法,幫助小明證明![]() .(一種方法即可)
.(一種方法即可)
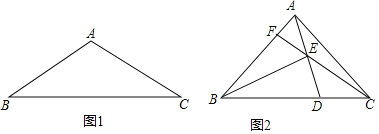
查看答案和解析>>
科目:初中數學 來源: 題型:
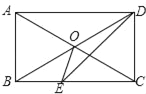
【題目】如圖,在四邊形ABCD中,AD∥BC,∠ABC=∠ADC=90°,對角線AC,BD交于點O,DE平分∠ADC交BC于點E,連接OE.
(1)求證:四邊形ABCD是矩形;
(2)若AB=2,求△OEC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“十二五”以來,北京市人口增長過快導致城市不堪重負,是造成交通擁堵,能源匱乏等“大城市病”的根源之一.右圖是根據北京市統計局近年各年末常住人口增長率及常住人口數的相關數據制作的統計圖.

有下面四個判斷:①從2011年至2016年,全市常住人口數在逐年下降; ②2010年末全市常住人口數達到近年來的最高值;③2015年末全市常住人口比2014年末增加18.9萬人;④從2011年到2016年全市常住人口的年增長率連續遞減。其中合理的是( )
A. ①② B. ①④ C. ②③ D. ③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與x軸交于點A(1,0),與 y交于點B(0,-2).
與x軸交于點A(1,0),與 y交于點B(0,-2).
(1)求直線AB的表達式;
(2)點C是直線AB上的點,且CA=AB,過動點P(m,0)且垂直于x軸的直線與直線AB 交于點D,若點D不在線段BC上,寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
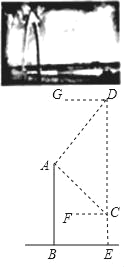
【題目】通達橋即小店汾河橋,是太原新建成的一座跨汾大橋,也是太原首座懸索橋.橋的主塔由曲線形拱門組成,取意“時代之門”.無人機社團的同學計劃利用無人機設備測量通達橋拱門的高度.如圖,他們先將無人機升至距離橋面50米高的點C處,測得橋的拱門最高點A的仰角∠ACF為30°,再將無人機從C處豎直向上升高200米到點D處,測得點A的俯角∠ADG為45°.已知點A,B,C,D,E在同一平面內,求通達橋拱門最高點A距離橋面BE的高度AB.(結果保留整數,參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
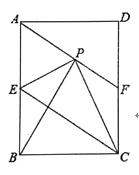
【題目】如圖,在矩形ABCD中,E是AB邊的中點,沿EC對折矩形ABCD,使B點落在點P處,折痕為EC,聯結AP并延長AP交CD于F點,
(1)求證:四邊形AECF為平行四邊形;
(2)如果PA=PC,聯結BP,求證:△APB![]() △EPC.
△EPC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com