Question

如圖，等腰梯形ABCD中，AB=4，CD=9，∠C=60°，動(dòng)點(diǎn)P從點(diǎn)C出發(fā)沿CD方向向點(diǎn)D運(yùn)動(dòng)，動(dòng)點(diǎn)Q同時(shí)以相同速度從點(diǎn)D出發(fā)沿DA方向向終點(diǎn)A運(yùn)動(dòng)，其中一個(gè)動(dòng)點(diǎn)到達(dá)端點(diǎn)時(shí)，另一個(gè)動(dòng)點(diǎn)也隨之停止運(yùn)動(dòng)．
（1）求AD的長；
（2）設(shè)CP=x，問當(dāng)x為何值時(shí)△PDQ的面積達(dá)到最大，并求出最大值；
（3）探究：在BC邊上是否存在點(diǎn)M使得四邊形PDQM是菱形？若存在，請(qǐng)找出點(diǎn)M，并求出BM的長；不存在，請(qǐng)說明理由．

Answer 1

【答案】分析：（1）可通過構(gòu)建直角三角形來求解：過A作AE⊥CD，垂足為E．那么可在直角三角形AED中根據(jù)兩底的差和∠D的度數(shù)來求出AD的長．
（也可通過作輔助線將梯形分成平行四邊形和等邊三角形兩部分來求解．）
（2）可通過求△PDQ的面積與x的函數(shù)關(guān)系式來得出△PDQ的最大值．由于P、Q速度相同，因此CP=QD=x，那么可用x表示出PD，而△PQD中，PD邊上的高=QD•sin60°，由此可根據(jù)三角形的面積公式求出S_△PQD與x之間的函數(shù)關(guān)系式，可根據(jù)函數(shù)的性質(zhì)求出S的最大值以及對(duì)應(yīng)的x的值．
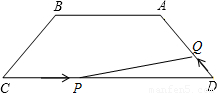
（3）假設(shè)存在這樣的M點(diǎn)，那么DM就是PQ的垂直平分線，可得出QD=PD、PM=AM，然后證PM=PD即可．根據(jù)（2）中得出PD、DQ的表達(dá)式，可求出x=，即P是CD的中點(diǎn)，不難得出△QPD為等邊三角形，因此∠QPD=∠C=60°，因此PQ∥CM，即∠DMC=90°，在直角三角形DMC中，P為斜邊CD的中點(diǎn)，因此PM=PD，即可得出四邊形PDQM是菱形．那么此時(shí)根據(jù)BM=BC-CM可求出BM的長．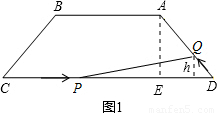
解答：解：（1）解法一：如圖1
過A作AE⊥CD，垂足為E．
依題意，DE==．
在Rt△ADE中，AD==．

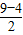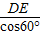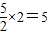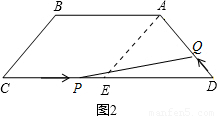解法二：如圖2
過點(diǎn)A作AE∥BC交CD于點(diǎn)E，則CE=AB=4．
∠AED=∠C=60度．
又∵∠D=∠C=60°，
∴△AED是等邊三角形．
∴AD=DE=9-4=5．

（2）如圖1
∵CP=x，h為PD邊上的高，依題意，
△PDQ的面積S可表示為：
S=PD•h=（9-x）•x•sin60°
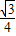=（9x-x²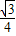）=-（x-）²+．
由題意知0≤x≤5．
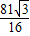當(dāng)x=時(shí)（滿足0≤x≤5），S_最大值=．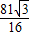

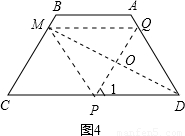（3）如圖4
存在滿足條件的點(diǎn)M，則PD必須等于DQ．
于是9-x=x，x=．
此時(shí)，點(diǎn)P、Q的位置如圖4所示，△PDQ恰為等邊三角形．
過點(diǎn)D作DO⊥PQ于點(diǎn)O，延長DO交BC于點(diǎn)M，連接PM、QM，則DM垂直平分PQ，
∴MP=MQ．
易知∠1=∠C．
∴PQ∥BC．
又∵DO⊥PQ，
∴MC⊥MD
∴MP=CD=PD
即MP=PD=DQ=QM
∴四邊形PDQM是菱形
所以存在滿足條件的點(diǎn)M，且BM=BC-MC=5-=．
點(diǎn)評(píng)：本題是一道壓軸題，也是一道開放探索題，第（2）問是條件開放，第（3）問是結(jié)論開放．本題既考查了學(xué)生的分析作圖能力，又考查學(xué)生綜合運(yùn)用平行線、等腰梯形、等邊三角形、菱形、二次函數(shù)等知識(shí)．這里設(shè)計(jì)了一個(gè)開放的、動(dòng)態(tài)的數(shù)學(xué)情境，為學(xué)生靈活運(yùn)用基礎(chǔ)知識(shí)、分析問題、解決問題留下了廣闊的探索、創(chuàng)新的思維空間．